４．プラントモデルの推定

　
　モデルベース開発で特に困難なのは，制御対象物のプラントモデリングです． その理由は，設計パラメータを含んだホワイトボックスモデルを，製品に合わせて作る必要があるからです．
　一方，プラント（制御対象）の設計変更や改良は行わず，制御設計だけ行うのであれば， 入出力関係だけを表現するブラックボックスモデルで十分です． その場合はシステム同定の技術を利用できます． プラントがSISO（単入力単出力）であれば，さらに易しくなります． matlabですと，System Identification Toolboxに色々な関数があって， これらを使えば，大体こと足ります． 少し頑張って自前の関数を作れば，System Identification Toolboxがなくてもシステム同定は可能です．
　さて，プラントが機械構造の場合，それを表現するホワイトボックスモデルは，ばねマスモデルになります． ところが，ばねマスモデルの推定に関しては特に有効な手段がないため， 試行錯誤を繰り返しながらモデルを調整するしかありませんでした．

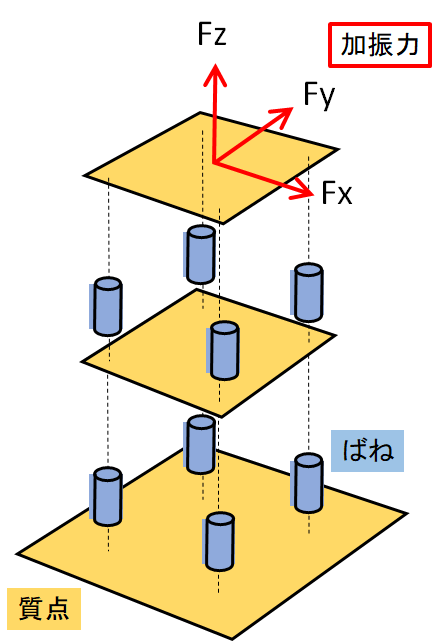
　そこで，実物を適切に表現したばねマスモデルの作成について取り組みました． 1990年頃からですから，かれこれ30年も経ちます．30年間ずっと，ばねマスモデルだけ扱っていた訳ではありませんが， 延べ10年間くらいは，この課題に取り組んでいました．それでも，満足できるモデルを手際よく作れたことは一度もありませんでした． いつも期限ぎりぎりまで，ばね剛性の調整を試行錯誤していました． もちろん，自動的に最適調整する方法は模索し続けました．
　特に，振動モード解析を利用した特性行列同定の方法には，色々な改良を試みました．論理的で最も良さそうだと，信じたからです． 実際，単純な構造で初期解が良ければ，期待通りのモデルになる場合もありました． しかし，構造が複雑になって剛体要素の数が増えると，期待通りのモデルは作れませんでした．
　そこで，振動モード解析への拘りを捨て，最近話題の人工知能を利用して再挑戦したところ， 意外と簡単に期待したばねマスモデルを作ることができました． しかし，いつでも期待したモデルを作れるとは限りませんでした．
　そこで，良い結果を得られる場合の傾向を調査したところ， 負荷のかけ方が静的になるほど推定精度が良くなることが分かりました． その理由は，微分方程式の加速度項も速度項もなくなり，線形方程式になるからです． 線形方程式であれば，誤差を含んでいても擬似逆行列で容易に解くことができます．
　しかし，実際の構造物に静的な負荷（加振力）を与えるには， 周辺に大規模な負荷機構を設置する必要があり，現実的ではありません． そこから，加振器だけで静的負荷実験と同質の実験データを得る二重正弦波加振法を考案しました． 以下に，詳しくご紹介します．

(1) 推定すべきは剛性である

　モデルベース開発の対象物であれば，大抵の場合はソリッドモデルがあります． たとえソリッドモデルになっていない配管や電装品やケーブルが付属していても， その部分だけ質量や慣性モーメントを計測できますから， わざわざ加振実験の結果から質量や慣性モーメントを推定する必要はありません． また，粘性については，そもそもモデルの特性としてあまり重要でないことが多い．
　一方，剛性については，部材同士を結合するボルトナットの緩みや， クラックなどの見えない欠陥によって，想定範囲外の結果となっている場合があり得ますから， 実験で推定する必要があります．

(2) 剛性の推定には，静的な伸縮実験が単純で良い

　ハンマーや加振器を用いた通常の加振実験は，対象構造の各質点が逆方向にも移動します． ばねは伸びているものもあれば縮んでいるものもあります． 右に示す動画では最上段に示した運動になります． これは，加振器による典型的な加振実験結果です．
　加振器による実験は手軽で良いのですが，通常は高周波振動も励起されます． 各質点が逆方向に動くような振動動作も発生しますから， データから剛性を推定するには，複雑な連立２階微分方程式を扱う必要があります． そして，この扱いが難しいため，ばねマスモデルの推定は思うようにゆきません．
　なぜ難しいかと言うと，微分方程式だからです． もしも加速度項と速度項がなくて位置だけでしたら，線形方程式ですので扱いは容易です． そして，理論上に限れば，加速度項と速度項をなくすことも簡単です． 静的な伸縮実験を行って，伸縮状態の異なる２つの状態で伸縮量と負荷を計測し，変化量を比較すれば良いのです．
振動実験は，式(1)のような連立2階微分方程式になります． $M$は質量行列，$C$は粘性行列，$K$は剛性行列で，$x$は位置ベクトル，$f$は加振力ベクトルを表します．

\begin{equation} M\ddot{x}+C\dot{x}+Kx=f \label{eq_mbd_1} \end{equation}
一方，伸縮実験であれば，線形方程式にすぎません．
\begin{equation} Kx=f \label{eq_mbd_2} \end{equation}

(3) 静的な伸縮動作（台形波）は非現実的

　静的な伸縮動作，つまり加速度と速度が一定時間零の状態を維持する場合を考えましょう． 上に示す動画の最下段をご覧下さい．2つの質点$m_{1}$と$m_{2}$は常に同じ方向に動き， 同時に静止して暫くしてから同時に動き始めます． なお，質点の枠が赤色になったときは静止していることを示しています． このように静止時間がある動作をさせる場合は，油圧シリンダのような負荷装置を用い， 装置の一部を固定物（地球）に結合する必要があります． また，その結合位置は作用力ベクトル上になければいけません． もし，直交する３方向に負荷をかける必要があれば， 大規模な支持構造物を準備する必要が生じます． この点が非現実的であることから，実際には行われないようです．

(4) 変位が単一周期の正弦波だと加速度と速度は同時に零とならない

　静的な伸縮実験が非現実的ならば，加振器を用いた動的な方法を用いることになります．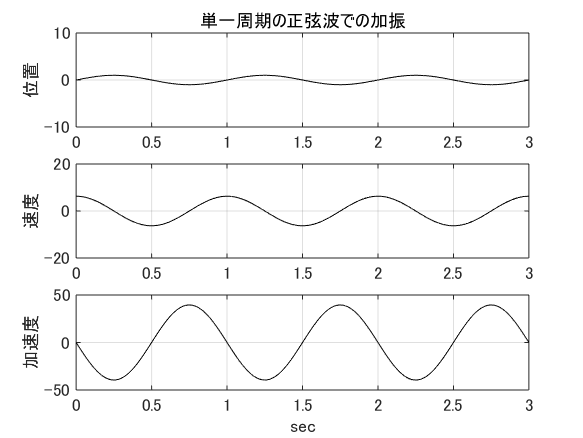 　
　最も素朴な方法は，長い単一周期の正弦波を加振力として与える方法です． 長周期の加振力に反応するのは，ばねの伸縮ですから， 位置の変化は正弦波に比例します． 正弦波を時間で微分すれば余弦波になります．
　つまり，速度は余弦波になり加速度は正弦波になります． 互いに位相が90度ずれた正弦波と余弦波は共に零になることはありません． この理由から，位置が単一周期の正弦波の場合，加速度と速度は同時に零とはなりません． また，共に正弦波である加速度と変位は同時に零となってしまいます．
　右図は単一周期の正弦波とそれを1回，2回微分したものを示しています． 先に示した動画では，上から2番目が単一周期の正弦波です． 両端で速度が零になりますが，加速度が零でないため赤枠で表示されることはありません． 単一周期の正弦波でも周期が極端に長ければ，速度も加速度も零に近づきます． でも，厳密には零になりませんし，そのような加振力を与える加振器は著しく巨大になり，非現実的です．

(5) 一瞬でも加速度と速度が零になれば良い

　たとえ一瞬でも，全質点の加速度と速度が同時に零となれば，その瞬間の加速度項と速度項は零になります． そういう瞬間のデータを収集すれば，静的な伸縮実験と同質のデータを得ることができます． つまり，加速度と速度が同時に零となる瞬間を持つ周期的な波形を作れればよい訳です． ただし，その瞬間の位置は少なくとも2種類なくてはいけません．
　さて，全質点の加速度と速度を同時に零とするには，全質点は同位相で運動している必要があります． さらに，ばねは伸縮しても振動モードは励起してはいけません． そのような加振力は最低次固有周期よりも周期の長い正弦波になります． そして，その加振力を伸縮力として各質点に与えれば，各ばねはそれに比例して伸縮します．

(6) 二重正弦波加振法の考案

　
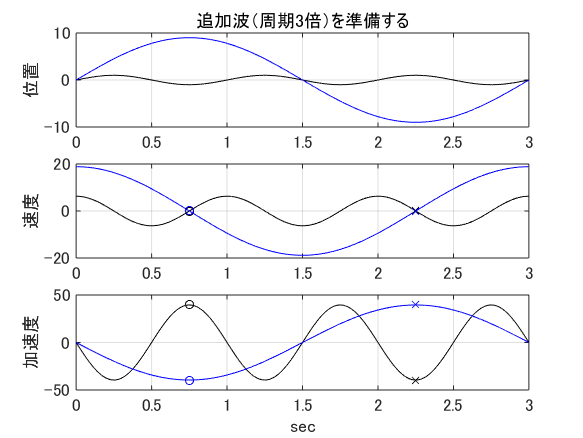
　変位が単一周期の正弦波であれば，加速度も変位も同時に零となります．しかし，周期の異なる正弦波を１つ加えれば，変位と加速度の同期は崩れます．
　これは，適切な周期と振幅の周期の正弦波を加えれば，所望の加振波を自由に作ることができることを示唆していることに気付きました．
　早速，周期と振幅を未知数として，速度と加速度が同時に零となる条件の連立方程式を立てて解きました．
　辿り着いた結果は意外と単純で，対象構造物の最低次固有周期よりも周期の長い加振波を基本波とし，以下の条件を満たす追加波を加算するだけでした．
　そこで，この方法を「二重正弦波加振法」と名付けました．

条件1：追加波の周期は基本波の$(4m-1)$倍である．ただし$m$は自然数
条件2：追加波の振幅は基本波の$(4m-1)^{2}$倍である．ただし$m$は自然数

　
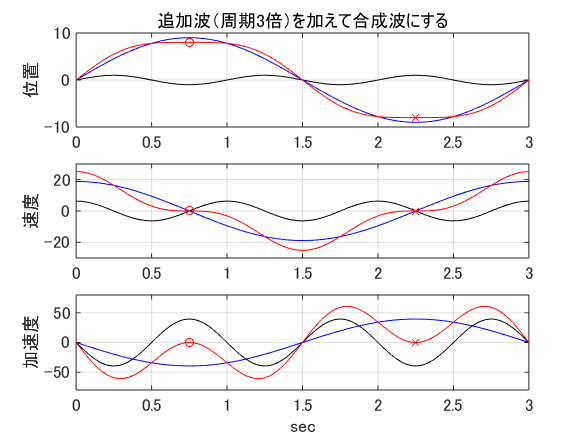
　例えば，$m=1$の場合，追加波は基本波に対して周期が3倍で振幅が9倍の正弦波になります．
　右の図は基本波と追加波の位置，速度，加速度を示しています． 黒い線は最低次固有周期よりも長い正弦波の基本波です． 青い線は追加波です．
　注目して頂きたいのは，基本波も追加波も速度が零になるとき，加速度の和が零になるようになっていることです．
　そういうタイミングは追加波の位相が丸印の$\pi/4$と×印の$3\pi/4$のときになります． ここでは，この2つのタイミングを時刻対と呼ぶことにします．
　時刻対における基本波と追加波の加速度は零ではありませんが，合算すると零になります． つまり，基本波と追加波を合算した合成波は，時刻対で速度も加速度も零になりますが， 位置は時刻対で異なります．
　それでは，基本波と追加波を合算した合成波を作り，上の図に合成波を重ね書きして下の図に示します． 赤線で示したのが合成波です．
　少し遡って，動画もご覧ください．下から2番目に二重正弦波と書いてあるものです． 最下段の静的伸縮と同じように，速度と加速度が同時に零になるので，一瞬ですが枠線が赤くなるときがあります．

(7) 二重正弦波加振法での剛性推定

　たとえ好条件のシミュレーションでも，通常の振動状態であれば，ばねマスモデルの剛性推定は良い結果になることはありませんでした． 一方，二重正弦波加振法であれば，普通に良い結果を得られるので，二重正弦波加振法を用いたばねマスモデルの剛性推定は有望であると言えます．
　実際，先に示した2階建構造のばねマスモデルについて，シミュレーションによる推定を行っていますので，紹介しておきます． 質量は2階が$100\rm{kg}$，屋上が$50\rm{kg}$で，慣性モーメントIxx,Iyy,Izzは2階が$10\rm{kgm}^2$，$100\rm{kgm}^2$，$1000\rm{kgm}^2$， 屋上が$5\rm{kgm}^2$，$50\rm{kgm}^2$，$500\rm{kgm}^2$で，Ixy,Iyz,Izxは2階も屋上も零にしました．
　各階を支える合計8本の柱には，各々3方向の剛性があるので，モデルは24本のばねで構成されることになります． これら24本のばねに12種類の剛性を割り当て，二重正弦波加振法の加振実験で得たデータから，この12種類の剛性を推定しました．
　下表は，割り当てた12種類の剛性の真値と推定結果を示していますが，推定誤差の小さいことが分かります．
　
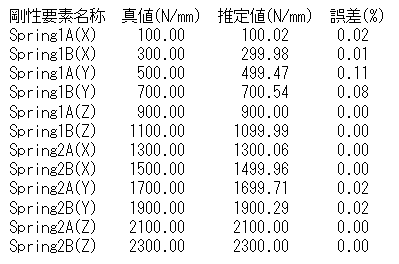
　さて、加振実験について説明しましょう．
　最初にシミュレーションモデルを利用して加振位置と加振方向を決めます． 加振する位置と方向は自由に決めて構いませんが 線形方程式の階数が未知な剛性要素の数と等しくなるようにします．
　こうして加振位置と加振方向が決まりましたら， 実物に通常の加振実験を行って周波数応答特性を計測します． 加振方法はランダム加振でも正弦波掃引でも構いません． この実験の主目的は，最低次固有振動周期を計測することですが， 振動モード解析まで行えば，モデルのマス（剛体要素）の分割箇所が適切であることを確認できます．
　
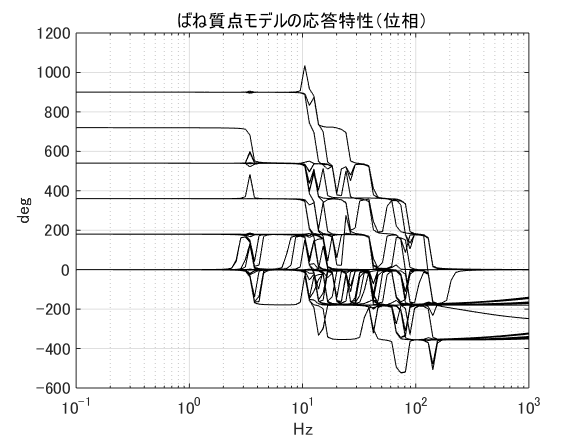
　右の図は，この加振実験で得た全ての周波数応答曲線の位相変化を示していますが， この図から，最低次固有振動数が2.5Hz辺りであることが分かります． 最低次固有周期はその逆数ですから，0.4秒となります．
　二重正弦波加振法で加振する場合，加振波の基本周期は最低次固有周期よりも長くします． 通常の振動動作を起こさないためです．
　しかし，長ければ良い訳でもありません．加振力は周期の2乗に比例して弱くなるからです． ここでは，基本波の周期を1秒．追加波の周期を3秒としました．
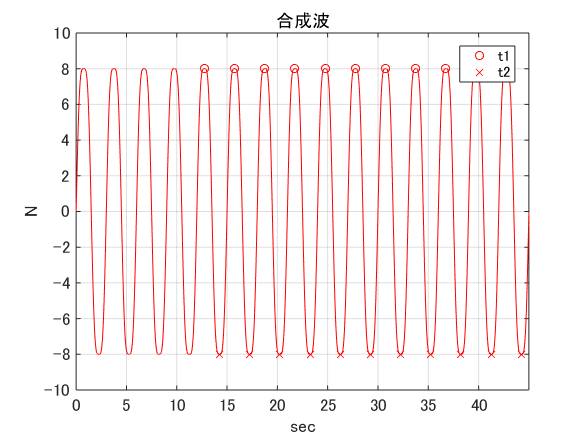
　右の図は、基本波と追加波を合せた合成波と，推定に使用した時刻対のデータを示しています． 開始から十数秒は高周波成分が減衰しないので，12秒以前のデータは推定に使用しませんでした．
　また，理論上は時刻対のデータは1組でも推定できますが， データを増やせば大数の法則によって計測誤差の影響を小さくできるので，時刻対は5つにしました．
　

(8) 今後の展望

　二重正弦波加振法による剛性推定の技術は，機構系プラントモデリングにとって有望であると確信し， 　2021年4月に特許出願手続を完了しています．
　しかし，実験での検証を行っていませんし，シミュレーションで検討すべきことはまだまだあります．
　少なくとも以下の課題を検討する必要があります．
①変位計測分解能と加振器仕様（出力とストローク）
　を考慮したシミュレーション
②計測ノイズと加振器出力誤差
　を考慮したシミュレーション
③加振位置と方向を適切に設定する方法
　（線形方程式の階数確保）の確立
　いずれにしても，弊社だけで研究を進めることは難しくなってきました．
　今後は，実験設備をお持ちで，モデルベース開発にご関心のある組織の皆さまと共同で進めたいと考えています． ぜひ，ご連絡ください．