ようこそ!数学屋ほん舗へ
 弊社は,数学応用力で社会貢献しようと始めた小さな会社です.いずれ優秀な後継者を加え,屈指の優良企業を目指しますが・・そのためには,数々の成果を挙げ,広く世間で活躍しなくてはなりません.
弊社は,数学応用力で社会貢献しようと始めた小さな会社です.いずれ優秀な後継者を加え,屈指の優良企業を目指しますが・・そのためには,数々の成果を挙げ,広く世間で活躍しなくてはなりません.そこでお願いがあります.ぜひ,数学屋ほん舗を利用して,大いなる成果を上げてください.それは,弊社が活躍の機会を得ることになります.数学屋ほん舗は,お客様の想像を超えた力を持っています.諦めかけた製品開発上の問題や課題を相談してみてください.数学とは無関係に思われた問題が,数学で解決した例は幾つもあります.
ここで挙げているMBD開発や半導体生産性,知的計測,最適化などの数学応用事業も,すべてはお客様の依頼から始まっています.起業前は半導体露光装置の経験が長いため,誤差に厳しい精密機械の実績が多いのですが,それ以外の課題でも大丈夫です.何でもできるわけではありませんが,結構期待して頂いて良いと思います.遠慮なく気軽にご相談ください.
写真は谷川岳一の倉沢です.厳しく過酷ですが,歩みを進めれば,この上なく美しい景色が待っています.そんな明るい希望をイメージしています.さあ,未来へ向かって一緒に進みましょう.
MBD開発(モデルベース開発)
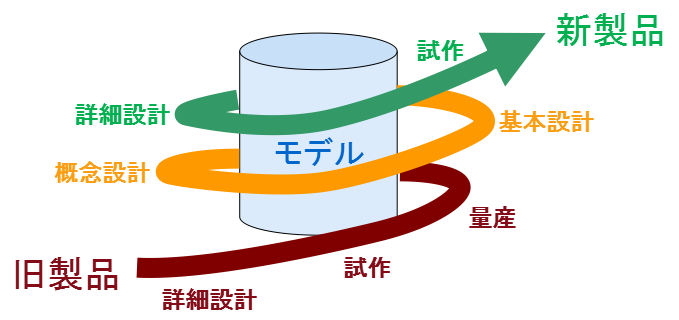 設計でシミュレーション(モデル)を利用するのは普通のことですが,設計後も途切れることなくシミュレーションを活用し続ける,次世代機種の概念設計にも利用するという,一歩進んだ開発が数学屋ほん舗のモデルベース開発です.シミュレーションで性能を確認したモデルを作り,そのモデルに実機を近づけるように開発するというモデル主体の思想は,補助的にシミュレーションを利用する従来のものとは異なります.
一方,最近流行のモデルベース開発は,自動車,宇宙開発,重機械などで,各々独自のモデルベース開発があり,かなり複雑です.また,CAE(計算機援用技術)との違いが分からないと言った声も聞きます.そこで,この違いを分かり易く説明しながら,数学屋ほん舗が推進するモデルベース開発について,実例を用いて紹介します.
設計でシミュレーション(モデル)を利用するのは普通のことですが,設計後も途切れることなくシミュレーションを活用し続ける,次世代機種の概念設計にも利用するという,一歩進んだ開発が数学屋ほん舗のモデルベース開発です.シミュレーションで性能を確認したモデルを作り,そのモデルに実機を近づけるように開発するというモデル主体の思想は,補助的にシミュレーションを利用する従来のものとは異なります.
一方,最近流行のモデルベース開発は,自動車,宇宙開発,重機械などで,各々独自のモデルベース開発があり,かなり複雑です.また,CAE(計算機援用技術)との違いが分からないと言った声も聞きます.そこで,この違いを分かり易く説明しながら,数学屋ほん舗が推進するモデルベース開発について,実例を用いて紹介します.
半導体生産性
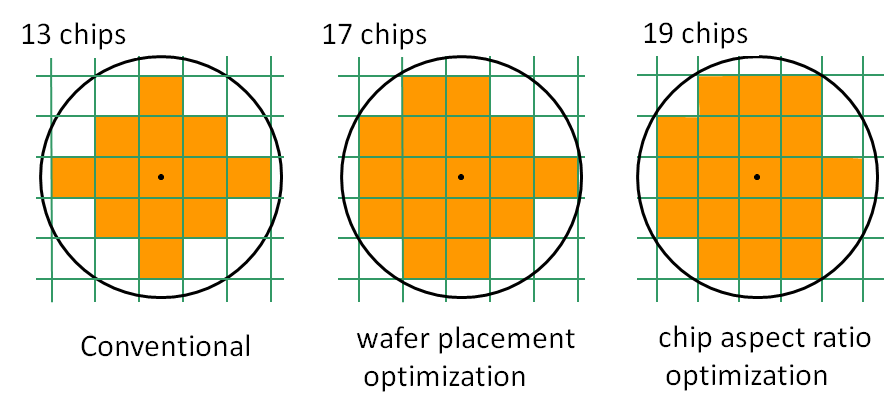 丸いウェーハから四角い半導体チップを切り出せば,どうしても捨てざるを得ない部分が発生します.この無駄な部分を極力少なくして,1つでも多くの半導体チップを得ようと言うのがこの技術です.最適化アルゴリズムのポイントや,これを利用して得られる効果などを分かり易く説明しています.とりわけ重要なのは,この最適化計算を本サイトの演算サービスページから容易に利用できることです.利用できるのは,チップ形状を最適化する縦横比最適化技術とチップの配置を最適化する配置最適化の2つの技術です.現在は普及推進活動に専念しているので,無料で使い放題です.
丸いウェーハから四角い半導体チップを切り出せば,どうしても捨てざるを得ない部分が発生します.この無駄な部分を極力少なくして,1つでも多くの半導体チップを得ようと言うのがこの技術です.最適化アルゴリズムのポイントや,これを利用して得られる効果などを分かり易く説明しています.とりわけ重要なのは,この最適化計算を本サイトの演算サービスページから容易に利用できることです.利用できるのは,チップ形状を最適化する縦横比最適化技術とチップの配置を最適化する配置最適化の2つの技術です.現在は普及推進活動に専念しているので,無料で使い放題です.その他の技術
 数学応用技術は意外なところで活躍してイノベーションを起こします.ここでは半導体露光装置での事例を紹介することで,数学応用技術の凄さを知って欲しいと思います.
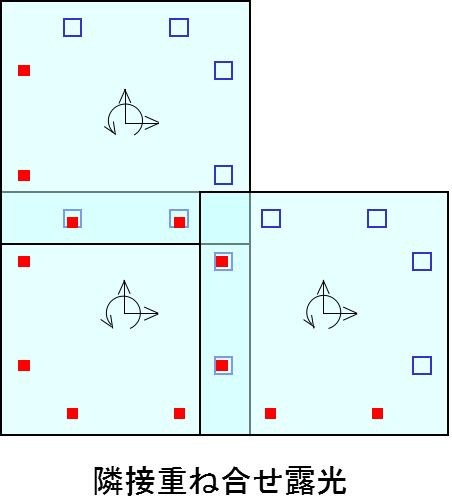
先ず紹介するのは,知的計測技術です.特に精密工学は正しく測ることが難しい分野ですが,干渉計や電子顕微鏡などのように,物理的に精緻化した技術だけでなく,知恵と工夫と数学で実現したソフトウェアデータムという計測技術もあります.また,誤差を細かく分類して高精度化の対策を導く統計解析も数学応用技術です.右図はテストパターン露光にソフトウェアデータムを利用した例を示しています.
次に紹介するのは,最適化技術です.特に現実的な最適化問題は,複数の制約条件の下で,ある性能をベストにしたいという場合が殆どです.ところが,意外にもこれに適した方法が知られていません.ここでは,これに適した「最大絶対値最小化法」の適用例を紹介します.
数学応用技術は意外なところで活躍してイノベーションを起こします.ここでは半導体露光装置での事例を紹介することで,数学応用技術の凄さを知って欲しいと思います.
先ず紹介するのは,知的計測技術です.特に精密工学は正しく測ることが難しい分野ですが,干渉計や電子顕微鏡などのように,物理的に精緻化した技術だけでなく,知恵と工夫と数学で実現したソフトウェアデータムという計測技術もあります.また,誤差を細かく分類して高精度化の対策を導く統計解析も数学応用技術です.右図はテストパターン露光にソフトウェアデータムを利用した例を示しています.
次に紹介するのは,最適化技術です.特に現実的な最適化問題は,複数の制約条件の下で,ある性能をベストにしたいという場合が殆どです.ところが,意外にもこれに適した方法が知られていません.ここでは,これに適した「最大絶対値最小化法」の適用例を紹介します.技術者の数学
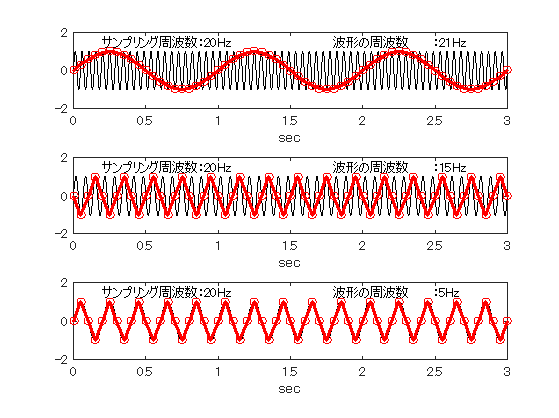 技術革新を実現した根本の技術は,適切な数学モデルで対象を表現することから始まっていることが多いものです.理由は簡単です.技術の対象や現象を説明する手段として,数学は最も適した表現手段(言語)だからです.しかし,数学を理解してから使おうとすると,なかなか前には進みません.むしろ,とりあえず色々な数学手法をつかってみて,その効果を体感した方が手っ取り早く理解できます.そこで,数学自体を理解することよりも,各種数学手法の利用効果を伝えることが,新たな技術革新につながると感じました.ここに掲載したのは,13章からなる数学手法の手引きです.まだ不十分な部分が多いと思いますが,読者の皆様と意見交換しながら,随時改編してゆくつもりです.右図は信号処理におけるサンプリング周期の影響を示しています.
技術革新を実現した根本の技術は,適切な数学モデルで対象を表現することから始まっていることが多いものです.理由は簡単です.技術の対象や現象を説明する手段として,数学は最も適した表現手段(言語)だからです.しかし,数学を理解してから使おうとすると,なかなか前には進みません.むしろ,とりあえず色々な数学手法をつかってみて,その効果を体感した方が手っ取り早く理解できます.そこで,数学自体を理解することよりも,各種数学手法の利用効果を伝えることが,新たな技術革新につながると感じました.ここに掲載したのは,13章からなる数学手法の手引きです.まだ不十分な部分が多いと思いますが,読者の皆様と意見交換しながら,随時改編してゆくつもりです.右図は信号処理におけるサンプリング周期の影響を示しています.(2019年 11月11日更新)
