第10章 伝達関数
伝達関数とは,入力と出力の伝わり具合と遅れの関係を示すラプラス演算子$s$の関数である. 本章では,伝達関数の数式とボーデ線図から,その特徴を把握する. こうした技術を身に付ければ,振動や制御の議論に参加できる.例として,式(\ref{Trns_eq1})の伝達関数を考える.
\begin{equation} H(s)=\frac{s+1}{s^{3}+12s^{2}+29s+90} \label{Trns_eq1} \end{equation} matlabが使えるなら, 次のように入力するだけで図10.1のようなボーデ線図が描ける.
>> sys=tf([0, 0, 1, 1],[1, 12, 29, 90])};
>> bode(sys);
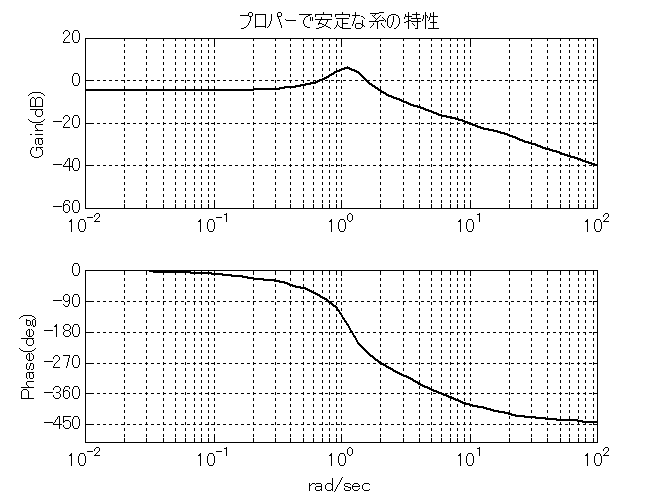
ただし,octaveの場合は,最初に以下のコマンドを実行しておく必要がある.
>> pkg load control
ステップ応答も簡単で,以下のコマンドを入力するだけで図10.2のステップ応答が描ける.
>> step(sys);
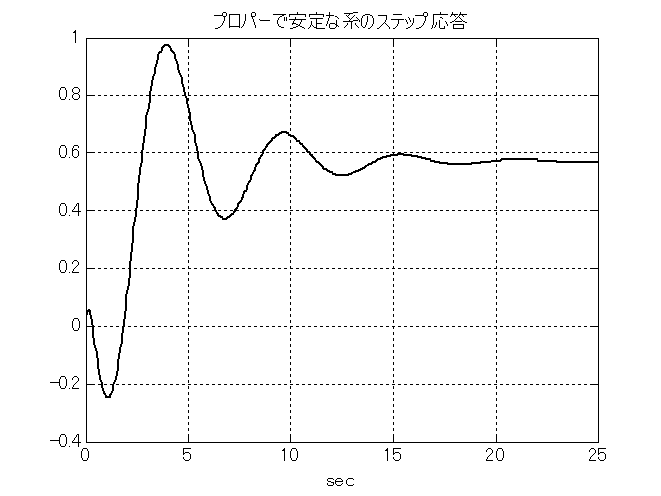
式(\ref{Trns_eq1})のように,分子の次数が分母より高くない伝達関数をプロパーな伝達関数と言う. プロパーでない系は実現できないから, 実際の伝達関数はプロパーで,かつ安定でなければならない.
10.1 3つの基本形
伝達関数はボーデ線図で示すのが一般的である.伝達関数$H(s)$からボーデ線図を描くには, $s=j\omega$を代入して$H(s)$の絶対値と複素平面での方位角を求めればよい. しかし,ここでは複素数を意識しないでボーデ線図をイメージする方法を述べる. それには,3つの基本形を知っているとよい.1次遅れ系
1次遅れ系は根が負の実数となる分母(ex.\ $s+a$)を持つ. また,$n$次遅れ系は1次遅れ系を$n$個掛け合わせたものである. 式(\ref{Trns_eq2})に伝達関数を, そのボーデ線図とステップ応答を図\ref{fig_Trns_3}と図\ref{fig_Trns_4}に示す.この系は熱伝導のモデルとしてよく用いられる. あるいは,高周波成分を除去するローパスフィルタとしても用いられる. 特に高周波振動を平滑化する目的のものをレギュレータと言う.
図\ref{fig_Trns_3}の伝達関数を見ると,低域のゲインは1で位相が0degだから,そのまま伝わっている. 一方,$\omega=a=1$のところでゲインが折れ曲がり,それより高域のゲインは\mbox{-20dB/デカード}で減少している. 位相は,$\omega=a=1$のところで-45degとなり,それより高域で-90degになる. つまり,高域の成分は伝わらなくなる.
$T=1/a$を時定数と呼び,ステップ波形が入力されると,時定数ぐらいで入力レベルの65\%程度に到達する.
ここで,ボーデ線図について簡単な説明をしておく. ゲインのグラフは,周波数毎の入出力振幅比を示す. 縦軸はdB(デシベル)という無次元の単位であり,$20\rm{log_{10}}\ (y)$という計算式で得られる. このように対数軸を用いると,系を直列に結合したときの伝達関数を容易に想像できるため便利である. 一方,位相は時間的な遅れを周波数毎の位相(角度)で示す.位相が180度異なるとき,入出力波形は逆向きの動作となる.
\begin{equation} H(s)=\frac{a}{s+a},\ \ \ a=1 \label{Trns_eq2} \end{equation}
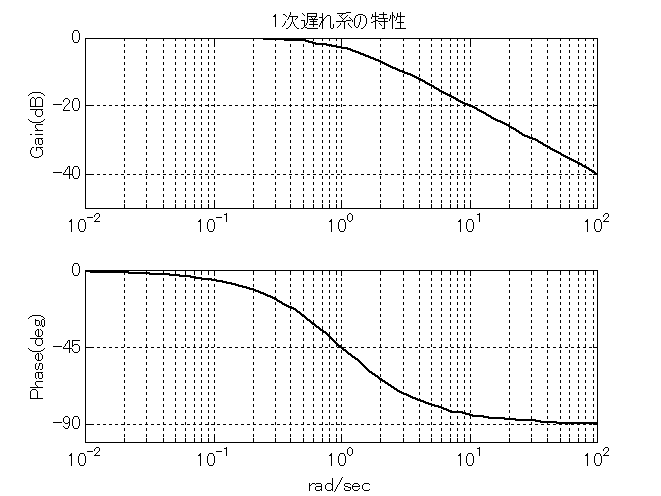
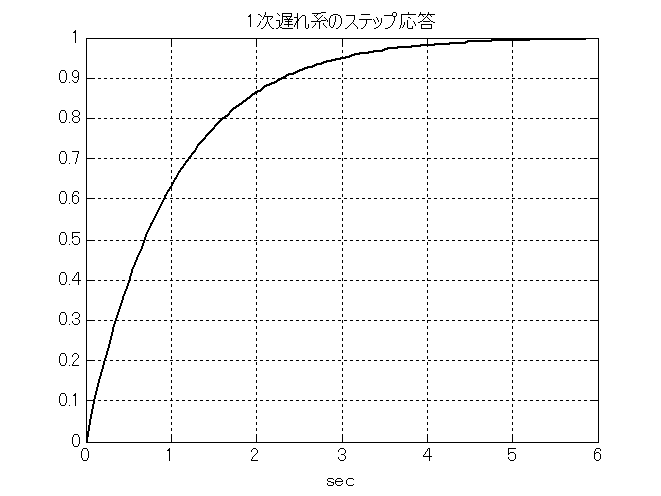
振動系
振動系の伝達関数は分母が2次関数の形になっている. 中学校で習った根の公式とか判別式を思い出してみよう. $4ac>b^{2}$だと複素根になり,伝達関数は振動的な挙動を持つ. そして,1次の係数が0で減衰のない自由振動系だと永久に振動し続ける. なお,除振台は固有振動数を越えるとゲインが急激に小さくなる振動系の特性を利用している. 式(\ref{Trns_eq3})に典型例を, その伝達関数とステップ応答を図\ref{fig_Trns_5}と図\ref{fig_Trns_6}に示す. ボーデ線図を見ると,低域のゲインは1で位相が0degだから,入力波形の低周波数成分はそのまま伝わる. 一方,$\omega=1$のところでゲインが折れ曲がり,それより高域のゲインは\mbox{-40dB/デカード}で減少している. 位相は,$\omega=1$のところで-90degとなり,それより高域で-180degになる. つまり,高周波数成分は伝わらない. \begin{equation} H(s)=\frac{1}{s^{2}+2\zeta \omega_{0} s+\omega_{0}^{2}},\ \ \ \zeta=0.05,\ \ \omega_{0}=1 \label{Trns_eq3} \end{equation}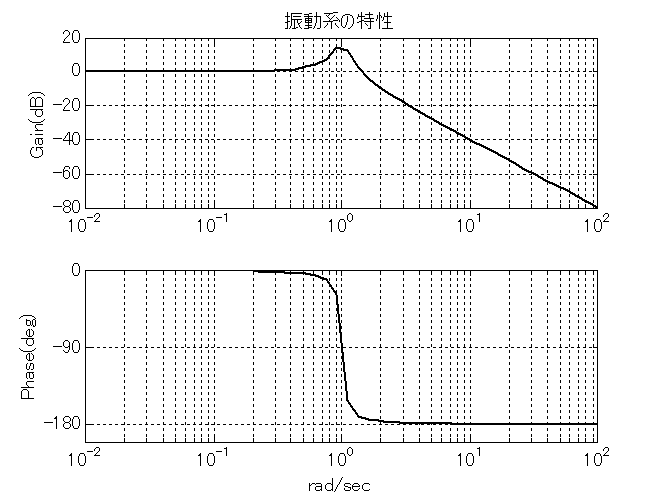
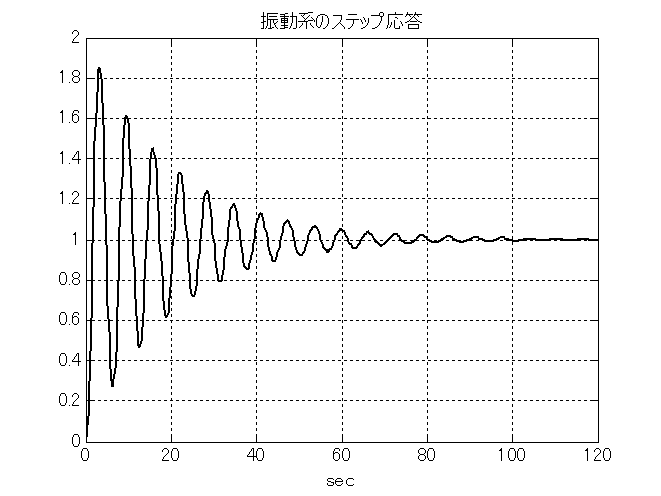
進み系
これは分子の次数が分母より高くプロパーでない.従って単独では存在しないが, 伝達関数を表現するために必要である. なお,進み系は位相を回復させるので,1次遅れと合わせて補償器(進み遅れ系)に用いる. 式(\ref{Trns_eq4})に伝達関数を, そのボーデ線図を図\ref{fig_Trns_7}に示す. 図\ref{fig_Trns_7}を見ると,低域のゲインは0dBであるが,$\omega=a=1$のところで折れ曲がり, それより高域では,20db/デカードで増加する. 位相は$\omega=0$のところで0degであるが,増加傾向にあって$\omega=a=1$のところで45degになり, それより高域になると90degに近づく. \begin{equation} H(s)=s+a,\ \ \ \ a=1 \label{Trns_eq4} \end{equation}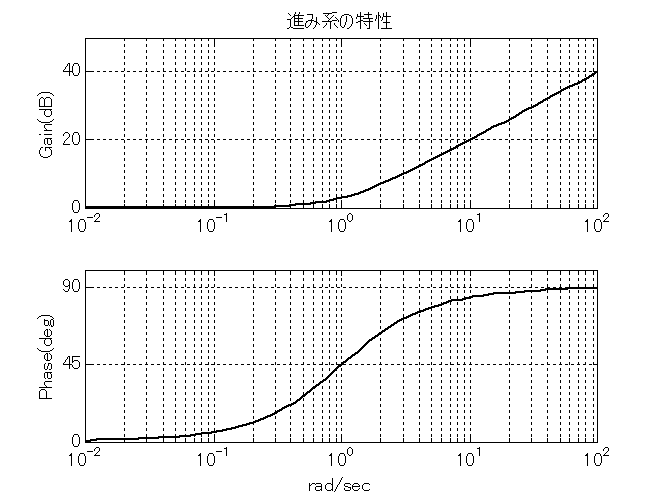
10.1 多項式を読む
matlabやmatlabを使えば,ボーデ線図は簡単に描ける. しかし,多項式形式だけでもある程度のことは読める. 後述する基本的な伝達関数の知識があれば,ボーデ線図の形を頭の中で描くこともできる. 式(\ref{Trns_eq1})を例に読んでみよう.低周波数域でのゲインと位相
0rad/sec付近の低周波数域は多項式で読める. 式(\ref{Trns_eq1})で$s=0$を代入すると,$H(0)=1/80$となる. dB表示すると$H(0)=20\log_{10}(1/80)=-38.06$となる.高周波数域でのゲイン
式(\ref{Trns_eq1})で$s=\infty$を代入すると,$H(\infty)=1/s^2=1/\infty=0$となる. つまり,周波数を高くしてゆくと$1/s^2$に近づく.そのため,周波数が10倍になるとゲインは40dBずつ小さくなる. もし,分子の次数が分母より$n$個少なければ,高周波域でのゲインは20$n$dBずつ小さくなる. 高周波域でのゲイン減少が大きければ,入力の高周波成分が伝わりにくくなる. もし,除振系の伝達関数であれば-40dB/デカードは欲しいところである.安定性
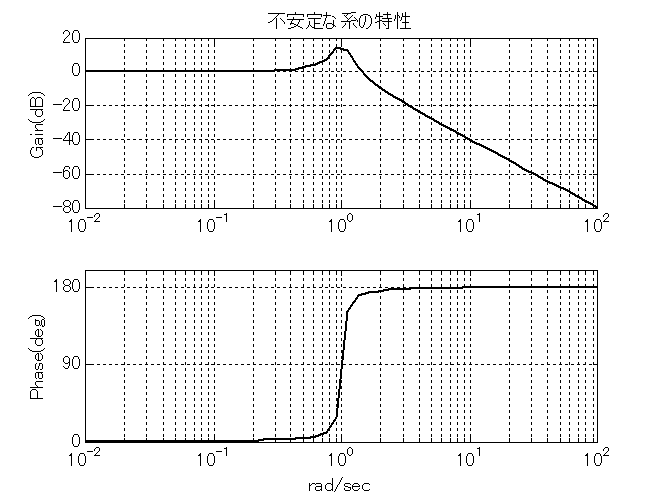
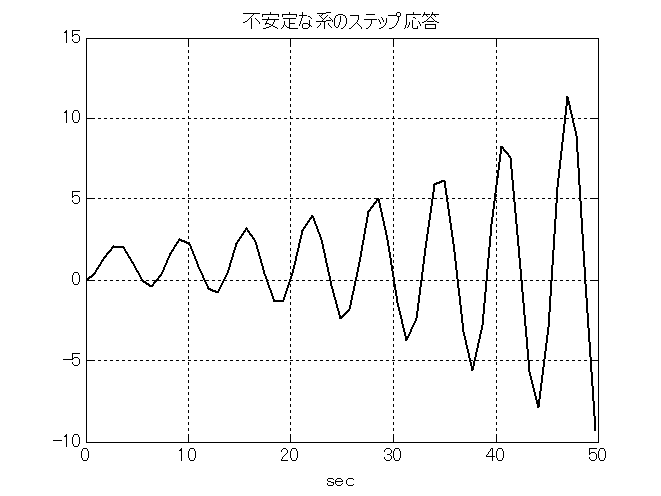
自然に発振するような系を不安定系という.逆に復元性のある系は安定系という. 不安定な系を見分けるには,分母に注目すればよい. \textbf{分母に1つでも異なる符号の項があれば不安定}である. また,\textbf{定数項が0のときも不安定}である. 不安定系の一例として発振する系を式(\ref{Trns_eq6})に, その伝達関数とステップ応答を図\ref{fig_Trns_8}と図\ref{fig_Trns_9}に示す. ステップ応答は,matlabなら\texttt{step(tf(1,[1 -0.1 1])}と入力すれば描ける. matlabなら,次のように入力する.>> t=[0.1:0.1:50]';
>> y1=csim('step',t,h1);
>> plot2d(t,y1);
\begin{equation} H(s)=\frac{1}{s^{2}-0.1s+1} \label{Trns_eq6} \end{equation}
10.2 極零形式を読む
伝達関数が式(\ref{Trns_eq1})のような多項式の形式であれば,周波数領域の両端部を把握できた. しかし,中間の周波数領域における特徴は把握できない. そのためには,極零形式に変換する必要がある. matlabなら,\texttt{zpk(tf([0 0 1 1],[1 12 29 90]))}と入力すればよい. すると,式(\ref{Trns_eq1})は式(\ref{Trns_eq7})の極零形式に変換される. ここで得られた分母の根を\textbf{極},分子の根を\textbf{零}と呼ぶ. なお,伝達関数の分子と分母に同じ極と零がある場合は約分して除いておく.\begin{equation} H(s)=\frac{s+1}{(s^{2}+2s+9)(s+10)} \label{Trns_eq7} \end{equation} 中間の周波数領域においてゲインと位相の変化を知るには,極零形式の伝達関数を式(\ref{Trns_eq8})のように 3つの基本形の積で表す.
\begin{equation} H(s)=(s+1) \times \frac{1}{s^{2}+2s+9} \times \frac{1}{s+10} \label{Trns_eq8} \end{equation} 式(\ref{Trns_eq8})は意図的に周波数の小さい順に並べてある. 以下に,順を追ってゲインと位相の変化を述べる.
1rad/sec付近
進み系があるから,ここで,ゲインは20dB/デカードの増加傾向となり90degの位相進みが発生する.3rad/sec付近
振動系の極があるので,ここで位相は-180deg遅れて-90degとなる. ゲインは,極のところで盛り上がり,-40dB/デカードの減少傾向となる筈だが, 進み系の影響があるので,減少傾向は-20dB/デカードにとどまる.10rad/sec付近
1次遅れ系があるので,-90degの位相遅れが生じて-180degとなる. ゲインは1次遅れ系の-20dB/デカードの減少傾向が加わり,全体で-40dB/デカードの減少傾向となる.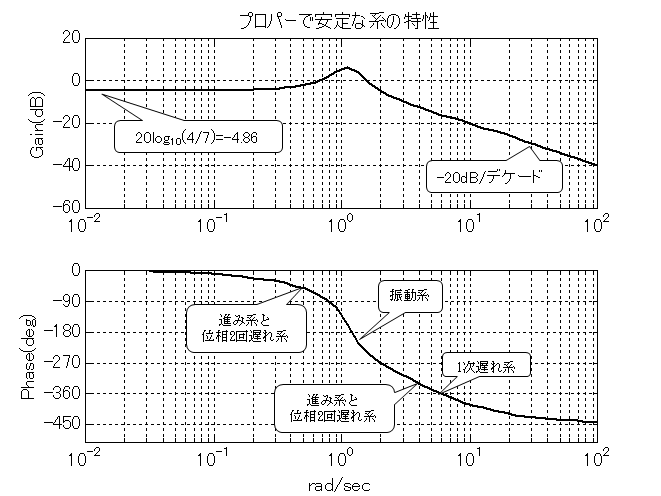
問題10.1
式(\ref{Trns_eq1})で用いた伝達関数のゲインを100倍にして,ステップ入力した10秒間の波形を示してください.(Simulinkを使える方のみ)
問題10.2
式(\ref{Trns_eq1})で用いた伝達関数のゲインを100倍にして,周波数1Hzで振幅1の正弦波を入力し10秒間計測した. 入出力波形を比較できるように示してください.(matlabの$\texttt{lsim}$を使ってシミュレーションする) また,ボーデ線図を参考にして,入出力の遅れ時間を示して下さい.問題10.3
進み遅れ系と呼ばれる補償器がある.これは次式のような伝達関数である. このボーデ線図を示してください. また,この伝達関数の低域から中間域,高域へとゲインと位相の変化を説明してください.\begin{equation} H(s)=\frac{s+1}{s+10} \notag \end{equation}
