第12章 制御系モデル
第11章では,機構系モデル図から運動方程式を立てる方法を学んだ. 本章では,機構部の運動方程式に制御部の運動方程式を加える. そして,ラプラス変換から各部の伝達関数を導いてブロック線図を描く. また,ブロック線図の等価変換則を学ぶ.これができるようになると,自分で伝達関数を求めることができる. 機構と制御のパラメータ(ex. $m$,$c$,$k$,$P$,$I$,$D$)を含んだ制御系のモデルは, 問題の原因や解決策を,機構と制御の両面から考える有効な手段である.
一方,振動モード解析は機構部の振動モデルを検討するのに有効である. モデルが妥当であれば必要ないが,固有振動数と振動モードでモデルを評価する ことが多いので,少しだけ触れておく.
12.1 ラプラス変換
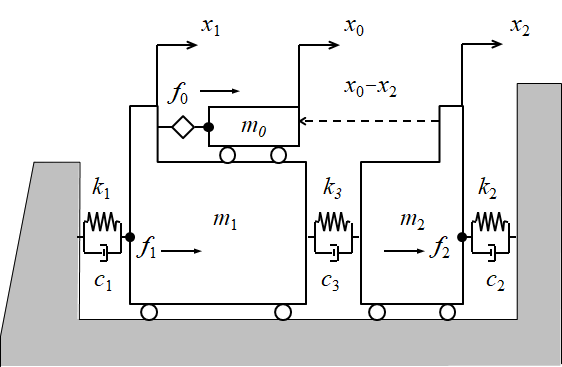
慣性項,粘性項,剛性項から構成された運動方程式に,ラプラス演算子$s$を導入する. ラプラス変換とは,指数関数による級数展開であるが,$x \rightarrow x$,$\dot{x} \rightarrow xs$, $\ddot{x} \rightarrow xs^{2}$という演算子を適用することだと思って差し支えない.例として,第\ref{Vibl}章でも示したKIC法の運動方程式を取り上げる. \begin{eqnarray} &&m_{0}\ddot{x_{0}} = f_{0} \label{Cont_eq1}\\ &&m_{1}\ddot{x_{1}} + c_{1}\dot{x}_{1} + c_{3}(\dot{x}_{1}-\dot{x}_{2}) + k_{1}x_{1} + k_{3}(x_{1}-x_{2}) =-f_{0} \label{Cont_eq2} \\ &&m_{2}\ddot{x_{2}} + c_{2}\dot{x}_{2} - c_{3}(\dot{x}_{1}-\dot{x}_{2}) + k_{2}x_{2} - k_{3}(x_{1}-x_{2}) =0 \label{Cont_eq3} \end{eqnarray} これらの式をラプラス変換すると,ラプラス演算子$s$の2次方程式になる. \begin{eqnarray} &&m_{0}x_{0}s^{2} = f_{0} \label{Cont_eq4} \\ &&m_{1}x_{1}s^{2} + c_{1}x_{1}s + c_{3}(x_{1}-x_{2})s + k_{1}x_{1} + k_{3}(x_{1}-x_{2}) =-f_{0} \label{Cont_eq5} \\ &&m_{2}x_{2}s^{2} + c_{2}x_{2}s - c_{3}(x_{1}-x_{2})s + k_{2}x_{2} - k_{3}(x_{1}-x_{2}) =0 \label{Cont_eq6} \end{eqnarray}
12.2 制御部のモデルとブロック線図
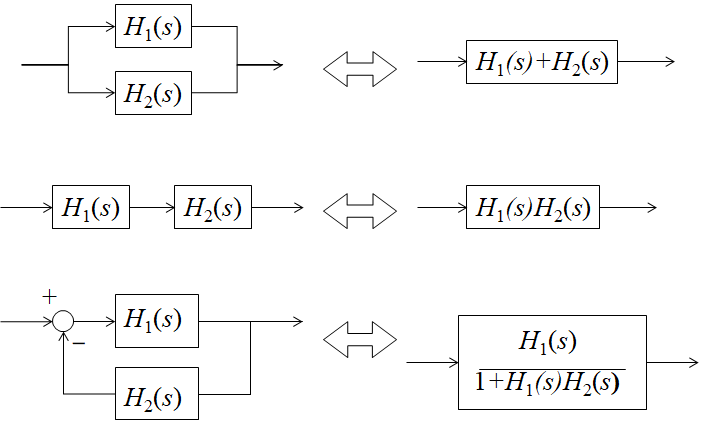
図11.2で示したモデルでは,計測したステージ位置が$x_{0}-x_{2}$であった.目標位置$r$と計測位置$x_{0}-x_{2}$ との差を$\textbf{制御偏差}$という.制御偏差$e$は式(\ref{Cont_eq7})で与えられる. \begin{equation} e=r-(x_{0}-x_{2}) \label{Cont_eq7} \end{equation} このとき,制御偏差$e$を零に近づけるように制御する. よく用いられる制御は,PID制御と呼ばれるもので,制御偏差$e$,その時間積分,時間微分の3つの線形和 で駆動力$f_{0}$をコントロールする.各々の係数を$P$,$I$,$D$とすれば,駆動力$f_{0}$は式(\ref{Cont_eq8})となる. \begin{eqnarray} f_{0}&=&(Ds+P+\frac{I}{s})\ e \notag \\ &=&(Ds+P+\frac{I}{s})\ (r-x_{0}+x_{2}) \label{Cont_eq8} \end{eqnarray} 式(\ref{Cont_eq4}),(\ref{Cont_eq8})から,ブロック線図を描くと図\ref{fig_Cont_1}のようになる. こうすれば,全体の構成や信号の流れが分かりやすくなる. また,図\ref{fig_Cont_2}の等価交換則を用いれば,ブロック線図を中をまとめたり分解することができる. なお,ブロック線図がループ状になったものをフィードバック制御系という.
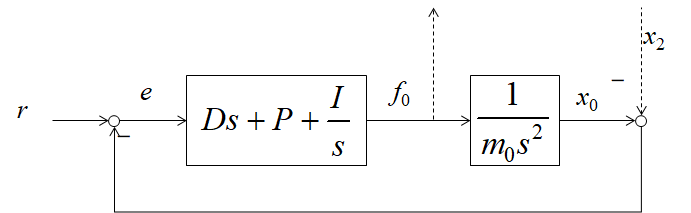
12.3 機構系の伝達関数
図12.1のブロック線図で,破線で示した矢印は本体定盤に作用する駆動反力$-f_0$と その出力である干渉計位置$x_2$を示しているから,描かれていない部分の本体定盤系を追加する必要がある.そこで,式(8.5),(8.6)を線形代数で示す.
\[\rightarrow \quad \left \{ \begin{matrix} s^2 m_1 x_1 + s(c_1+c_3) x_1 -s c_3 x_2 +(k_1+k_3) x_1 -k_3 x_2 =-f_0 \\ s^2 m_2 x_2 -s c_3 x_1 + s(c_2+c_3) x_2 -k_3 x_1 +(k_2+k_3) x_2 =~0~~~ \end{matrix} \right .\] \[\rightarrow \quad s^2 \left [ \begin{matrix} m_1 & 0 \\ 0 & m_2 \end{matrix} \right ] \left \lgroup \begin{matrix} x_1 \\ x_2 \end{matrix} \right \rgroup +s \left [ \begin{matrix} c_1+c_3 & -c_3 \\ -c_3 & c_2+c_3 \end{matrix} \right ] \left \lgroup \begin{matrix} x_1 \\ x_2 \end{matrix} \right \rgroup + \left [ \begin{matrix} k_1+k_3 & -k_3 \\ -k_3 & k_2+k_3 \end{matrix} \right ] \left \lgroup \begin{matrix} x_1 \\ x_2 \end{matrix} \right \rgroup = \left \lgroup \begin{matrix} -f_0 \\ 0 \end{matrix} \right \rgroup \] \[\rightarrow \quad \left \lgroup s^2 \left [ \begin{matrix} m_1 & 0 \\ 0 & m_2 \end{matrix} \right ] +s \left [ \begin{matrix} c_1+c_3 & -c_3 \\ -c_3 & c_2+c_3 \end{matrix} \right ] + \left [ \begin{matrix} k_1+k_3 & -k_3 \\ -k_3 & k_2+k_3 \end{matrix} \right ] \right \rgroup \left \lgroup \begin{matrix} x_1 \\ x_2 \end{matrix} \right \rgroup = \left \lgroup \begin{matrix} -f_0 \\ 0 \end{matrix} \right \rgroup \] ここで,以下のように{\bf 特性行列}$\bf{M},\bf{C},\bf{K}$,列ベクトル$\bf{x},\bf{f}$を定義すれば 式(\ref{Cont_eq9})のように略記できる. \[ \bf{M}:= \left [ \begin{matrix} m_1 & 0 \\ 0 & m_2 \end{matrix} \right ] ,\bf{C}:= \left [ \begin{matrix} c_1+c_3 & -c_3 \\ -c_3 & c_2+c_3 \end{matrix} \right ] ,\bf{K}:= \left [ \begin{matrix} k_1+k_3 & -k_3 \\ -k_3 & k_2+k_3 \end{matrix} \right ] ,\bf{x}:= \left \lgroup \begin{matrix} x_1 \\ x_2 \end{matrix} \right \rgroup ,\bf{f}:= \left \lgroup \begin{matrix} -f_0 \\ 0 \end{matrix} \right \rgroup \] \begin{eqnarray} [\ s^{2}\bf{M} + s\bf{C} + \bf{K} ]\ \bf{x} =\bf{f} \label{Cont_eq9}\\ \rightarrow \qquad s^{2} \bf{M} x+s\bf{Cx}+\bf{Kx}=\bf{f} \notag \\ \rightarrow \qquad s\bf{M} s\bf{x}+\bf{C}s\bf{x}+\bf{Kx}=\bf{f} \notag \\ \rightarrow \qquad (s\bf{M} +\bf{C})\ s\bf{x}+\bf{Kx}=\bf{f}\notag \end{eqnarray} 列ベクトル$\left \lgroup \begin{matrix} s\bf{x} \\ \bf{x} \end{matrix} \right \rgroup $を用いて表すと,以下のようになる.ここで$\bf{0}$はスカラーではなく,$\bf{M},\bf{C},\bf{K}$と同サイズの零行列である. \begin{eqnarray} \rightarrow \qquad \left [ \begin{matrix} s\bf{M} +\bf{C} & \bf{K} \end{matrix} \right ] \left \lgroup \begin{matrix} s\bf{x} \\ \bf{x} \end{matrix} \right \rgroup=\bf{f} \notag \\ \rightarrow \qquad \left [ s\left [ \begin{matrix} \bf{M} & \bf{0} \end{matrix} \right ] + \left [ \begin{matrix} \bf{C} & \bf{K} \end{matrix} \right ] \right ] \left \lgroup \begin{matrix} s\bf{x} \\ \bf{x} \end{matrix} \right \rgroup=\bf{f} \notag \end{eqnarray} これと,以下の自明な式を上下に並べて合わせる. \begin{eqnarray} s\bf{Mx}-\bf{M}s\bf{x}=\bf{0} \quad \rightarrow \quad \left [ s \left [ \begin{matrix} \bf{0} & \bf{M} \end{matrix} \right ] + \left [ \begin{matrix} -\bf{M} & \bf{0} \end{matrix} \right ] \right ] \left \lgroup \begin{matrix} s\bf{x} \\ \bf{x} \end{matrix} \right \rgroup =\bf{0} \notag \\ %\[ \left [ s \left [ \begin{matrix} \bf{M} & \bf{0} \\ \bf{0} & \bf{M} \end{matrix} \right ] + \left [ \begin{matrix} \bf{C} & \bf{K} \\ -\bf{M} & \bf{0} \end{matrix} \right ] \right ] \left \lgroup \begin{matrix} s\bf{x} \\ \bf{x} \end{matrix} \right \rgroup = \left \lgroup \begin{matrix} \bf{f} \\ \bf{0} \end{matrix} \right \rgroup \label{Cont_eq10} %\eqno(8.10)\] \end{eqnarray} $\bf{M}$は対角行列だから正則で逆行列$\bf{M}^{-1}$をもつ. 式(\ref{Cont_eq10})の両辺に左から行列$\left [ \begin{matrix} \bf{M}^{-1} & \bf{0} \\ \bf{0} & \bf{M}^{-1}\end{matrix} \right ] $ をかけて次のように書き換えられる.なお,$\bf{I}$は$\bf{M},\bf{C},\bf{K}$と同サイズの単位行列である. \begin{eqnarray} \left [ s \left [ \begin{matrix} \bf{I} & \bf{0} \\ \bf{0} & \bf{I} \end{matrix} \right ] + \left [ \begin{matrix} \bf{M}^{-1} \bf{C} & \bf{M}^{-1} \bf{K} \\ -\bf{I} & \bf{0} \end{matrix} \right ] \right ] \left \lgroup \begin{matrix} s\bf{x} \\ \bf{x} \end{matrix} \right \rgroup = \left \lgroup \begin{matrix} \bf{M}^{-1}\bf{f} \\ \bf{0} \end{matrix} \right \rgroup \label{Cont_eq11} \end{eqnarray} まず,状態空間表現で用いる行列$\bf{A}$を次のように定義する. \begin{equation} \bf{A}:= \left [ \begin{matrix} -\bf{M}^{-1} \bf{C} & -\bf{M}^{-1} \bf{K} \\ \bf{I} & \bf{0} \end{matrix} \right ] \label{Cont_eq12} \end{equation} 状態空間表現で用いる行列$\bf{A}$の固有値解析によって振動モード解析ができる. 振動系の伝達関数を導くだけなら,振動モード解析は必要ない. しかし,振動モデルの妥当性を確かめたり修正するのに役立つ. さて,$\bf{A}$の固有値解析$[\bf{V},\bf{\Lambda}]=\rm{eig}(\bf{A})$で得られる固有値ベクトル群$\bf{V}$と 固有値行列$\bf{\Lambda}$は, $\bf{V}^{-1}\bf{AV}=\bf{\Lambda}$という関係がある.これは主成分分析でも示した. 同様に,固有値解析を用いて振動モード解析を行う.
まず,モード変数$z$と入力ベクトル$g$を定義しておく.
\begin{equation} \bf{z}:=\bf{V}^{-1} \left \lgroup \begin{matrix} s\bf{x} \\ \bf{x} \end{matrix} \right \rgroup すなわち, \bf{Vz}= \left \lgroup \begin{matrix} s\bf{x} \\ \bf{x} \end{matrix} \right \rgroup \label{Cont_eq13} \end{equation} \begin{equation} \quad g:= \bf{V}^{-1} \left \lgroup \begin{matrix} \bf{M}^{-1} \bf{f} \\ \bf{0} \end{matrix} \right \rgroup すなわち, \bf{Vg}= \left \lgroup \begin{matrix} \bf{M}^{-1} \bf{f} \\ \bf{0} \end{matrix} \right \rgroup \label{Cont_eq14} \end{equation} 式(\ref{Cont_eq11})に$\bf{A},\bf{Vz},\bf{Vg}$を代入し, $\left [ \begin{matrix} \bf{I} & \bf{0} \\ \bf{0} &\bf{I} \end{matrix} \right ] $をあらためて$\bf{I}$と表すと,次のようになる.
\begin{equation} (s\bf{I}-\bf{A})\bf{Vz}=\bf{Vg} \label{Cont_eq15} \end{equation} 両辺に左から$\bf{V}^{-1}$をかけて, \begin{eqnarray} \bf{V}^{-1}(s\bf{I}-\bf{A})\bf{Vz}=\bf{V}^{-1}\bf{Vg} \notag \\ \rightarrow \quad (s\bf{V}^{-1}\bf{IV}-\bf{V}^{-1}\bf{AV})\bf{z}=\bf{g} \notag \end{eqnarray} $\bf{V}^{-1}\bf{AV}=\Lambda$より,
\begin{equation} \rightarrow \quad (s\bf{I}-\bf{\Lambda})\bf{z}=\bf{g} \label{Cont_eq16} \end{equation} $(s\bf{I}-\bf{\Lambda})$は対角行列になっていて,固有振動数の異なるモード毎に分解されている. \begin{equation} (s-\bf{\Lambda}_{ii}) \bf{z}_i=\bf{g}_i \notag \end{equation} これが振動モード解析である. なお,$\bf{V}$は,固有振動数毎の振動モードを示している. さて,本題に戻ろう. 状態空間表現には,入力箇所を定める$\bf{B}$,出力箇所を定める$\bf{C}$, 入力から直接伝達する成分量を定める$\bf{D}$の行列が必要である. この場合,$\bf{B}$は式(\ref{Cont_eq11})の右辺から求められる.
\begin{equation} \bf{B}= \left( \begin{array}{c} -1/m_{0} \\ 0 \\ 0 \\ 0 \\ \end{array} \right) \label{Cont_eq17} \end{equation} $\bf{C}$は,状態変数$(\dot{x_{1}},\dot{x_{2}},x_{1},x_{2})$から出力する変数を引き出す行ベクトル だから,$x_{1}$を出力したいなら$\bf{C}$は,式(\ref{Cont_eq18})になる.
\begin{equation} \bf{C}= [\ 0,0,1,0\ ] \label{Cont_eq18} \end{equation} $\bf{D}$は,入力から出力まで直接伝達する成分の量を示す.この場合は0である. このように,状態空間表現の行列$\bf{A}$,$\bf{B}$,$\bf{C}$,$\bf{D}$を作れば,matlabで簡単に伝達関数を求める ことができる. 次にmatlabのサンプルプログラムを示す.
***************************************************
>> % パラメータの定義
>> m1 = 8000;% kg
>> m2 = 1000;% kg
>> c1 = 400000;% Ns/m
>> c2 = 400000;% Ns/m
>> c3 = 800000;% Ns/m
>> k1 = 4000000;% N/m
>> k2 = 4000000;% N/m
>> k3 = 4000000000;% N/m
>> % 特性行列を作る
>> M = [m1,0;0,m2];
>> C = [c1+c3,-c3;-c3,c2+c3];
>> K = [k1+k3,-k3;-k3,k2+k3];
>> % 状態空間表現にする
>> [row,col]= size(M);
>> A = [-inv(M)*C,-inv(M)*K;eye(row,col),zeros(row,col)];
>> B = [-1/m1,0,0,0]';
>> C1 = [0,0,1,0];
>> C2 = [0,0,0,1];
>> % MATLAB(ss,tf)を使って伝達関数を求める
>> Hfx1 = syslin('c',A,B,C1);% fからx1までの状態空間表現
>> Hfx2 = syslin('c',A,B,C2);% fからx2までの状態空間表現
>> ss2tf(Hfx1)% fからx1までの伝達関数
>> ss2tf(Hfx2)% fからx2までの伝達関数
***************************************************
このプログラムを動作させると,\texttt{tf(Hfx1)}と\texttt{tf(Hfx2)}の命令で伝達関数が表示される.
- 500.49917 - 0.1500009$s$ - 0.0001250$s^2$
--------------------------------------------------
4.002D+09 + 4.012D+08$s$ + 4604500$s^2$ + 1350$s^3$ + $s^4$
- 500.00049 - 0.0999979$s$ - 2.046D-12$s^2$
--------------------------------------------------
4.002D+09 + 4.012D+08s + 4604500$s^2$ + 1350$s^ 3$ + $s^4$
12.4 制御系の伝達関数
前節までに,機構部と制御部の部分的な伝達関数を求める方法とブロック線図の等価変換を学んだ. ここでは,機構部と制御部を合体した$\textbf{制御系}$の伝達関数を求める.さて,$\textbf{伝達関数}$とは入力から出力までの伝わり具合を示す関数である. KIC法のモデルで言えば,入力には,ステージの指令位置$r$,床振動,計測ノイズなどが考えられる. また,出力には,干渉計基準のステージ位置$x_{0}-x_{2}$,制御偏差$e=r-x_{0}+x_{2}$, スコープ計測値$x_{0}-x_{1}$などが挙げられる.
ここでは,ステージの指令位置$r$からスコープ計測値$x_{0}-x_{1}$までの伝達関数を導く. まず,モデル図を見ながらブロック線図を描いてみる. 各ブロックの配置など気にせず,入出力にだけ気をつけて描く.
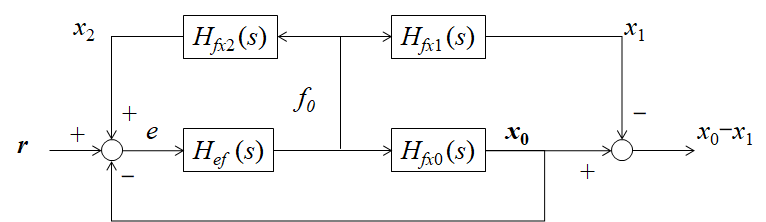
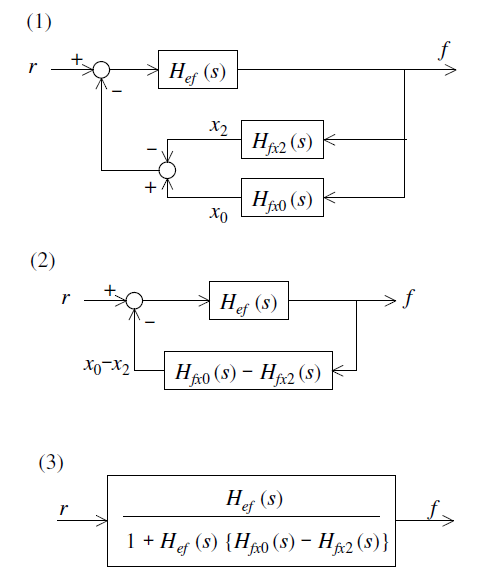
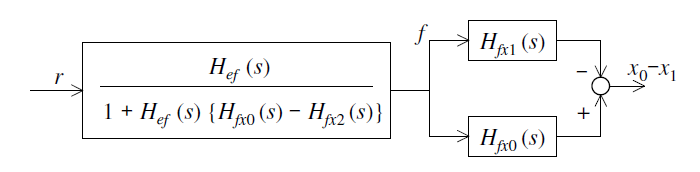
初めに,$r$から$f$までの伝達関数を求めてみる. 図\ref{fig_Cont_4}は(1)から(3)まで,等価変換によってまとめて行く様子を示している. $r$から$x_{0}-x_{1}$までの伝達関数は,図\ref{fig_Cont_5}で表される. まとめてしまえば,結局,式(\ref{Cont_eq19})で表される. \begin{equation} x_{0}-x_{1}=\frac{H_{ef}(H_{fx0}-H_{fx1})}{1-H_{ef}(H_{fx0}-H_{fx2})}r \label{Cont_eq19} \end{equation} なお,ブロック線図の等価交換を用いなくても, $x_{0}$,$x_{1}$,$x_{2}$,$f$,$e$についての連立方程式を解いても良い.