第5章 統計的検定
検定とは,データから判断を下すための手法である.その手順は以下の3段階で構成される.- 仮説(帰無仮説)を立てる
- 仮説を前提として,適当な事象や統計量の発生確率を求める
- 余りにも発生確率が低いときは,仮説を否定する
次に重要なのは,確率を計算する事象や統計量の設定である. 現実問題で,データの分布型が分かっている場合は稀である. 従って,分布型を気にしなくて済むノンパラメトリック検定はお奨めである. 中でも順位和検定と順位相関検定の簡単な公式を使えば,大半の検定問題は片付く. また,ノンパラメトリック検定は,異常値に対してもロバスト(影響を受けにくい)であるという特長もある.
初めは,ノンパラメトリック検定の使い方を知るだけでも良い. しかし,できれば,この方法が中心極限定理を上手く利用している ことを理解して欲しいので,ノンパラメトリック検定と中心極限定理の 関係について,独自の解説を試みたいと思う.
5.1 帰無仮説
「帰無仮説」とは何とも哲学的な言い回しで理解しにくいが,「差がない」「関係がない」という仮説であると理解しておけば良い.「どうして帰無仮説なのか?」と言うと,そうでない仮説は無限に存在して検定できなかったり, 検定できても計算が厄介になるからである.また,「どうして厄介になのか?」と言うと,仮説の中に範囲を示す表現が入るからである. 「差がある」「関係がある」と書くと,”どれくらい”という意味が含まれてしまう. そうなると,その範囲について検定する必要が生じ,厄介になるのである.
例えば,計測誤差が $\sigma$ =1mの正規分布に従うとき,A山の高さの計測値は103.0mであったとする. このとき,「A山の高さxは100m以上である」という仮説を立てたとすると, 仮説が成立する確率は,次の式で計算することになる.
\begin{equation} prob(x \geq 100)=\frac{1}{\sqrt{2\pi}}\int_{100}^{\infty}exp\ \Bigl( -\frac{(x-103)^{2}}{2}\Bigr)\ dx \notag \end{equation} この場合,仮説成立の確率は計算できるが,積分があるため計算は厄介になる. 一方,「A山の高さxは100mである」という仮説を立てたとすると,計測値の103mは $\mu+3\sigma$ に相当し, 正規分布表から,0.1\%程度の確率でしか起こらない事象であることが分かる. つまり,範囲を持つ事象でなく範囲を持たない事象を仮説にすると,検定は容易になる.
5.2 ノンパラメトリック検定
ノンパラメトリックというのは,母数(例えば $\mu$,$\sigma$ )を用いないという意味らしい. 多くの本では,「データの分布型を気にしなくて良い検定方法」と定義されている. 要するに,母集団の分布が正規分布でも一様分布でも何でも構わないのである. これは特殊な事のように聞こえるが,そうではない. むしろ,予め分布関数型が分っていると仮定する方が特殊である.根拠も無く「正規分布だとする・・」などといい加減な仮定をしてはいけない. 分らないものは,分らないとして扱うべきである. そう考えれば,ノンパラメトリック検定の正当性を理解できるであろう.
また,ノンパラメトリック検定のもう1つの長所は,異常値(外れ値)の影響を受け難い ロバスト性があることである.これは,データを数値でなく順位で扱うことによる.
ところで,多くの統計的検定における命題は,同一性(差がない)と 独立性(関係がない)のいずれかである. 実際,これまでの経験でそれ以外の検定をした記憶は無い.
また,検定というのは,たかがYESかNOかの選択に過ぎないから, よほどデータが少ない場合を除き,データの持つ全ての情報を使わなくても問題はない. それよりも,「異常値判定」などの主観的操作は避けた方が良い.
このような観点からも,ノンパラメトリック検定(順位和,順位相関)は大変良い方法なのである.
順位和検定
これは,2つのデータ群について同一性を検定する方法である. A群のデータが $m$ 個,B群のデータが $n$ 個あったとき, それらをまとめて,小さい方から順に1,2,\ ...,\ $m+n$ の番号を付ける.そして,A群のデータについて順位数の和$U$を求める.このとき, $m$ と $n$ が大きければ,$U$ の分布は正規分布で近似できて, その平均 $\mu (U)$ と分散 $\sigma^{2} (U)$ は式(\ref{eqTest_1}),(\ref{eqTest_2})で表される.
つまり,順位和 $U$ が著しく大きいあるいは小さい場合に,仮説を棄却することができる.
\begin{eqnarray} \mu (U) = \frac{m(m+n+1)}{2} \label{eqTest_1}\\ \sigma^{2} (U) = \frac{mn(m+n+1)}{12} \label{eqTest_2} \end{eqnarray} 式(\ref{eqTest_3})で,標準正規分布に従うZスコアを求めれば,もっと分りやすい. \begin{equation} Z=\frac{U-\mu(U)}{\sigma (U)} \label{eqTest_3} \end{equation} 例として,A群データの順位が[1,2,3,4,5],B群データの順位が[6,7,\ ...\ ,15]であったとき, Zスコアを求めてみよう.まず, \begin{equation} U = 1+2+3+4+5 = 15 \notag \end{equation} 式(\ref{eqTest_1}),(\ref{eqTest_2})より, \begin{eqnarray} \mu (U) &=& 5\times (5+10+1)/2=40 \notag \\ \sigma (U) &=& \sqrt{5\times 10\times (5+10+1)/12} = 20/\sqrt{6} \notag \end{eqnarray} よって, \begin{eqnarray} Z = (15-40)\times \sqrt{6}/20 = -3.06 \notag \end{eqnarray} このとき,$Z$ の絶対値は3以上なので,仮説を棄却して,A群はB群と同じでないと結論付けてよかろう.
ところで,データ数 $m$ と $n$ はどれくらい必要なのだろうか?
これは,色々な組合せの $m$ と $n$ について,実際にシミュレーションで順位和の分布を求め, それが正規分布に近いかどうかで判断すればよい. 図5.1は,$m=n=4$ のときの順位和から求めたZスコアの分布を示している. 実線は参考に示した標準正規分布の曲線である. これより,有意水準が1\%,3\%,5\%のどれでも,概ね正確に検定できる. 従って,順位和検定なら $m,n \geq 4$ であれば可能であろう.
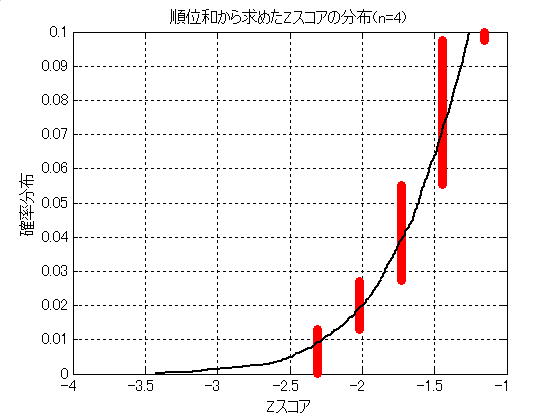
順位相関検定
2つのデータ群における独立性をノンパラメトリック検定するには,順位相関係数を用いる.いま,対応する2種類の数値データ $(x_{i},y_{i}),\ i=1,2,...,n$ があるとき,各種のデータを各々小さい順に順位数をつけ, 順位データ $(Rx_{i},Ry_{i}),\ i=1,2,...,n$ を作ったとすると, 順位相関係数 $\rho$ は,式(\ref{eqTest_5})で求められる.
\begin{eqnarray} V &=& Rx_{1}Ry_{1}+ Rx_{2}Ry_{2}+ ... +Rx_{n}Ry_{n} \label{eqTest_4}\\ \rho &=& \frac{V-n(n+1)^{2}/4}{n(n^{2}-1)/12} \label{eqTest_5} \end{eqnarray} 竹内啓の著書「数理統計学」(東洋経済)では, 「2つのデータ群が互いに独立(無関係)で $n \geq 10$ であれば,$\rho$ は 平均 $\mu=0$,分散 $\sigma ^{2}=1/(n-1)$ の正規分布で近似できる」と書かれている.
つまり,順位相関係数に $\sqrt{n-1}$ を乗じればZスコアとなり,容易に独立性の検定ができる. 小生のシミュレーションだと,検定に使うだけなら $n \geq 6$ でも十分だと思う.
図5.2は,$n=6$ のときの順位相関から求めたZスコアの分布を示している. 実線は標準正規分布の曲線である. これより,有意水準が3\%,5\%なら十分に検定できる. 従って,順位相関なら $n \geq 6$ でも検定可能である.
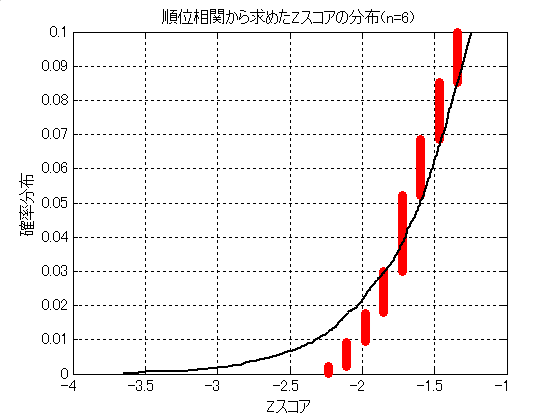
中心極限定理
$x_{1},x_{2},...,x_{n}$ が平均 $\mu$,分散 $\sigma^{2}$ が同じ確率分布に従う互いに独立な変数であるとき, \begin{equation} \bar{x}=\frac{1}{n}(x_{1}+x_{2}+...+x_{n})\label{eqTest_6} \end{equation} とすると,$n$ が大きくなるとき,$\bar{x}$ の分布は(元の分布が何であっても)正規分布に近づく. 正確には,式(\ref{eqTest_7})で定義された統計量 $z$ は,漸近的に標準正規分布 $N(0,1)$ に従う. これを,中心極限定理という. \begin{equation} z=\frac{\sqrt{n}(\bar{x}-\mu)}{\sigma}\label{eqTest_7} \end{equation} ところで,順位和検定は中心極限定理をとても巧妙に使っている. これに気付けば,ノンパラメトリック検定が理路整然とした素晴らしい方法であることが分る.少し具体的に言おう.一様乱数を数個足し合わせれば正規分布の乱数として使える ことを知っているだろうか?(6個で十分と言われている) これも中心極限定理を使ったものである. データ数を増すと急激に正規分布に近づく様子は,感動的でさえある. 是非とも実際に確かめると良い.
ところで,順位数の分布も一様である.一様に分布した順位数からランダムに $m$ 個の順位数を取り出して 総和を求めるのは,ノンパラメトリック(分布型によらない)と言っておきながら, 実は,中心極限定理を用いて,正規分布となる統計量を作り出している. これは一様乱数から正規乱数を作るのと殆ど同じである.
