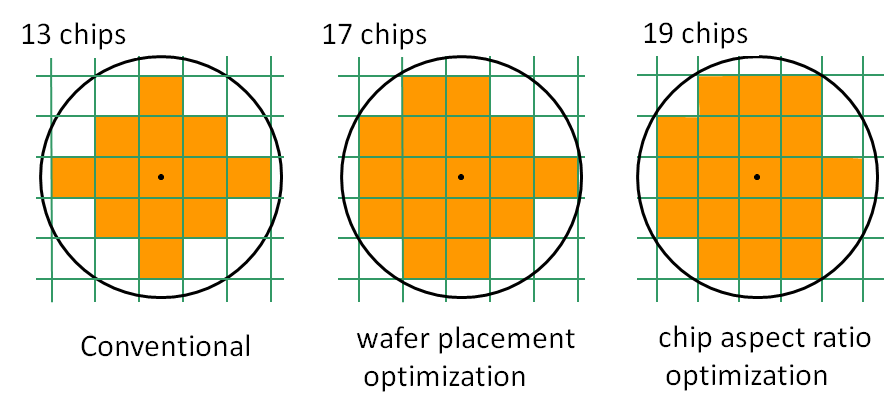
左端の図は，ウェーハ中心を正方形のチップ中心に配置した基準状態の一例です．この場合，有効チップ数は13個ですが，ウェーハ配置を適切に変化させることで，有効チップ数を増やすことができます．この方法で有効チップ数を最大にすることを配置最適化と呼びます．
　簡単な方法としては，チップ内の複数箇所にウェーハを配置して，有効チップ数が最大となる場合を選ぶ方法が考えられます．
　配置最適化の場合は，この方法でも十分に実用的です．中央の図は，チップ縦横比はそのままに，ウェーハ配置だけを最適化して有効チップ数を17個にまで増やした場合を示しています．さらに，正方形チップの面積は変えずに，縦横比とウェーハ配置の両方を調整すると，右図のように有効チップ数を19個まで増やすことが出来ます．これを縦横比最適化と呼んでいます．
　縦横比最適化は，配置最適化の自由度であるウェーハ位置の2自由度に，チップの縦横比の1自由度を加えた問題です．従って，配置最適化よりも有効チップ数が多くなることが期待できます．しかし，最適化によってチップ縦横比を決定できるのは，半導体のレイアウト設計ですから，チップ形状が決まった後で行うことはできません．また，実際の半導体レイアウト設計において，チップ面積を一定に保ちながら自由に縦横比を選択できるとは考えにくい．従って，縦横比の場合は，縦横比と有効チップ数の関係を把握した中で，実現可能で有効チップ数の多い縦横比を設計者が選択することになります．

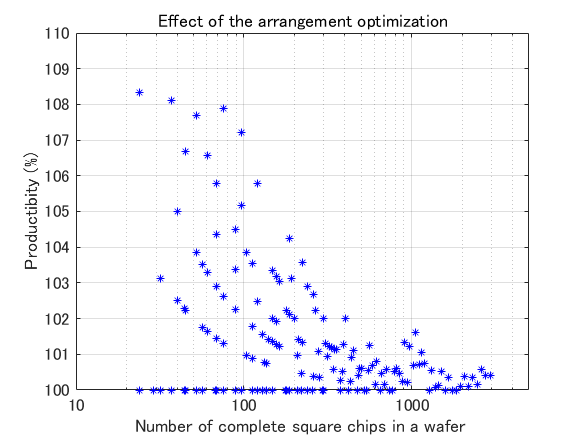
　右の図は，ウェーハ中心にチップ中心かチップ角のいずれかを選ぶ 2点法に対して，配置最適化したときの生産性を示しています．横軸は，2点法で得られる有効チップ数であり，縦軸はウェーハ配置を最適化したときの生産性を示しています．なお，生産性が 100% のときは，2点法の結果がベストであることを意味しています．
　この図から，有効チップ数が 500個以上ですと生産性向上の効果は 0.5% 程度しか見込めません．一方，有効チップ数が 100個～500個の範囲であれば，3% 程度の効果が期待でき，100個未満であれば 6% 程度の効果が見込めます．
　なお，生産性が 100% の意味は，2点法の結果がたまたま最適配置であることを意味しています．また，そのような場合は約 25% ありました．

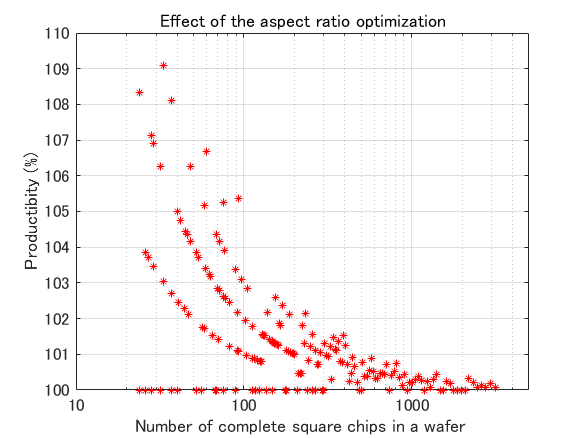
　右の図は，チップ縦横比が 1，つまり正方形のチップ形状に対して，面積を変えずに縦横比だけ最適化したときの生産性を示しています．具体的には，横軸がウェーハ配置を最適化した正方形チップの有効チップ数，縦軸がチップ縦横比を最適化することで増加した有効チップ数の割合を示しています．
　多くの人は，正方形が最良のチップ形状であると直感的に信じています．実際，右図のシミュレーションでも約 40% は正方形がベストであるという結果でしたから，その直感が大間違いとは言えませんが，残りの 60% は，正方形でない長方形がベストであるという結果は，それ自体が大きな驚きであると思います．
　なお，チップ縦横比を最適化することの効果ですが，有効チップ数が 100個未満の場合は 5% 程度，500個未満でも 1% 程度の効果が期待できます．ウェーハ配置最適化に比べると小さいように思われますが，比較の基準は正方形チップで配置最適化してある状態ですから，2点法で配置した場合と比較するのであれば，配置最適化と縦横比最適化の両方の効果を合算することになり，非常に大きな生産性向上になります．

利用動向

　本サービスの運用は，配置最適化が2017年11月，縦横比最適化が2018年9月に運用を開始しました．
　配置最適化は，以前より多くの半導体メーカーで独自の方法で実施されているようで，敢えて弊社の方法を利用されるメーカー様はいませんでした．一方，縦横比最適化に関しては，そもそ縦横比は1が良いと考えている人の方が多いですし，レイアウト設計の工程でのみ利用可能ですから，利用対象者の人数は余り多くありません．そのような理由もあって，余り利用されていませんが，それでも最近は少しずつ増加しています．
　しかし，弊社のような外部サイトにアクセスし，半導体の設計情報を入力することはできないと，利用を諦めている方がおられます．そもそも，入力情報と言っても，設計値に該当するのはチップ面積だけで，まだ決定もしていない値です．他にも，インバリッドエリア，ウェーハ直径，オリフラ長なども入力しますが，これらの値が持つ機密性が高いとは思えません．ですから，情報流出の心配は，それ自体が存在しないと思われます．
　それでもまだ心配でしたら，実際には使わない条件のものを複数選んで入力してみてください．容易にカモフラージュできます．