(5) バネマスモデルの同定
実のところ,満足できるレベルのバネマスモデル同定技術を獲得したのは,つい最近のことです.それまでは,1つ1つパラメータ(主に剛性)を調整していました.同定と言うよりは,手作業によるすり合わせでした.
一方,同定技術の重要性に気づいたのは30年ほど前です.30年間ずっと研究していた訳ではありませんが,それでも延べ数年間は試行錯誤していたと思います. 随分と長い時間がかかりましたが,諦めなくて良かったと思います.
まず,モデルベース開発における主な同定技術について,少しだけお話ししましょう.
対象が化学物質の場合であれば「同定」は分類のことですが,ここでは,制御対象(プラント)を数学的に表現することになります.
一般的な同定とは,制御対象の入出力応答信号から伝達関数(数学モデル)を導くシステム同定になります. matlabですと,System Identification Toolboxに色々な関数があって,これらを使えば,大体こと足りるようです. ただし,頑張って自前の関数を作れば,System Identification Toolboxがなくてもシステム同定は可能です.
そして,制御対象のシステム同定ができれば,制御設計も可能です. つまり,制御対象はそのままで,ただ制御設計だけするのであれば,既存のシステム同定技術で十分です.
しかし,制御対象も設計対象である場合,つまり,機構と制御の同時設計を行う場合ですと,システム同定では不十分です. なぜなら,システム同定で導いた伝達関数には,制御対象の設計パラメータが含まれていないため,設計変更できないからです.
ここで,制御対象の設計パラメータを含んだ伝達関数のことを物理モデルと呼び,システム同定の数学モデルと区別します. 制御対象がロボットアームや自動車のような機構の場合,物理モデルは質量,粘性,剛性などの要素で構成した数式で表現できます. これをバネマスモデルと言います.
バネマスモデルを線形代数で示すと質量行列,粘性行列,剛性行列で構成される微分方程式になりますが,これは特性行列と呼ばれます. つまり,バネマスモデルと特性行列は,ほぼ同じものです.
特性行列の同定技術に関しては,古くから大熊政明先生(東工大)の研究が知られていて,数多くの論文があります. 最近では,質量行列だけを同定する研究成果が報告されています.
私も大熊先生の論文を読み,その方法を真似してきました.教えを乞いに何度かお伺いしたこともあります. しかし,私の能力不足もあり,安定した同定結果を得られないまま30年が過ぎました.
そして今回,最近話題のAI技術を意識し,剛性行列だけの同定に挑戦したところ,計測ノイズにも影響されにくく安定した同定手法に辿り着きました. 特許出願前であるため,まだ詳しいことは書けませんが,例題を示すことで,同定技術のレベルをお示ししようと思います.
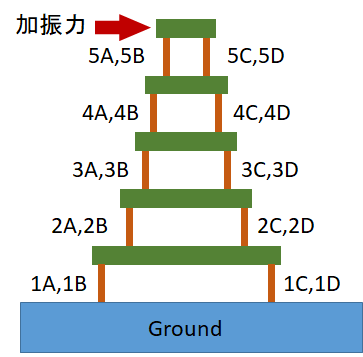
例題は,3方向の剛性(ばね)を持つ4本の柱で各階を支えた5階建構造としています.(右図)
その最上階で,前後左右上下(xyz)の各方向に加振力(チャープ信号)を与え,各階中心の6自由度変位を計測します.
そして,加振力と変位のデータから柱の弾性(kx,ky,kz)を同定するというものです.
この場合,未知の剛性要素は60個になります.
60個=3方向×4本×5階
なお,各階の質量と慣性モーメント,剛性は下表のように既知とします.

質量や慣性モーメントは,階が上に行くほど軽く,逆に剛性は上に行くほど大きくしました. その値の範囲は100N/mm~60000N/mmまでです.固有振動数のピークが1Hz~1000Hzの範囲に分布するようにしました. 最初,各々の剛性値は等差級数にしていたので,全て異なっていました. しかし,同定すると,各階の振動波形は一致しましたが,表に示した剛性値に収束ました. つまり,同じ応答特性になる60個の剛性値の組合せは,必ずしも1種類とは限らないようです.
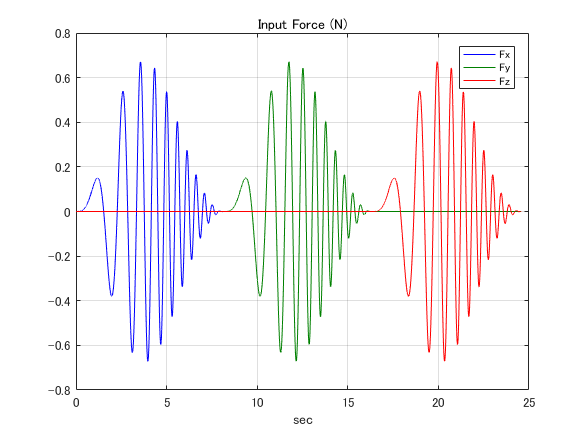
次に,収束した値を真の剛性値にしてみると,同定した結果は真の剛性値と同じになりました. 今後,一意の解が得られるようにするための実験方法を考える必要はありますが, 大きな問題ではないと判断し,真の剛性値に収束する剛性値の組み合わせを選んでいます. さて,このバネマスモデル同定で実現したいことは,個々の剛性値に対する予備知識がなくても,未知である剛性値を安定的に同定することです. そこで,全ての剛性要素の初期値を 1.0e+8 N/mm と高く設定しました.つまり,ガチガチに固い状態を想定しました. 最上階に与えるチャープ信号の加振力は,最初の8秒間がx方向,次の8秒間がy方向,最後の8秒間がz方向です.
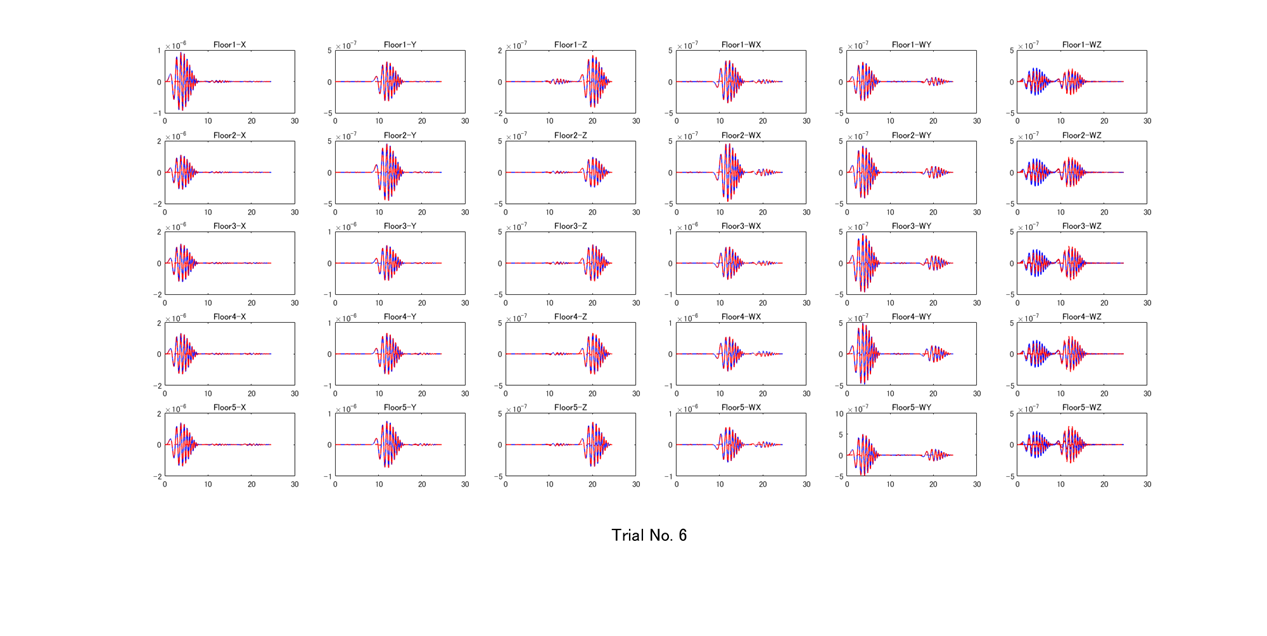
それでは,最初に試行した結果を下図に示します.左から右に向かって各階重心位置における変位(m)x,y,z,と角度(rad)wx,wy,wzを示しています.1段目は1階,5段目は5階です. 青い線は真のモデルから求めた出力信号です.一方,赤い線は同定結果です.最初は全ての剛性値を高くしていますから,同定結果(赤線)の変位や角度はいずれも零に近い状態です.
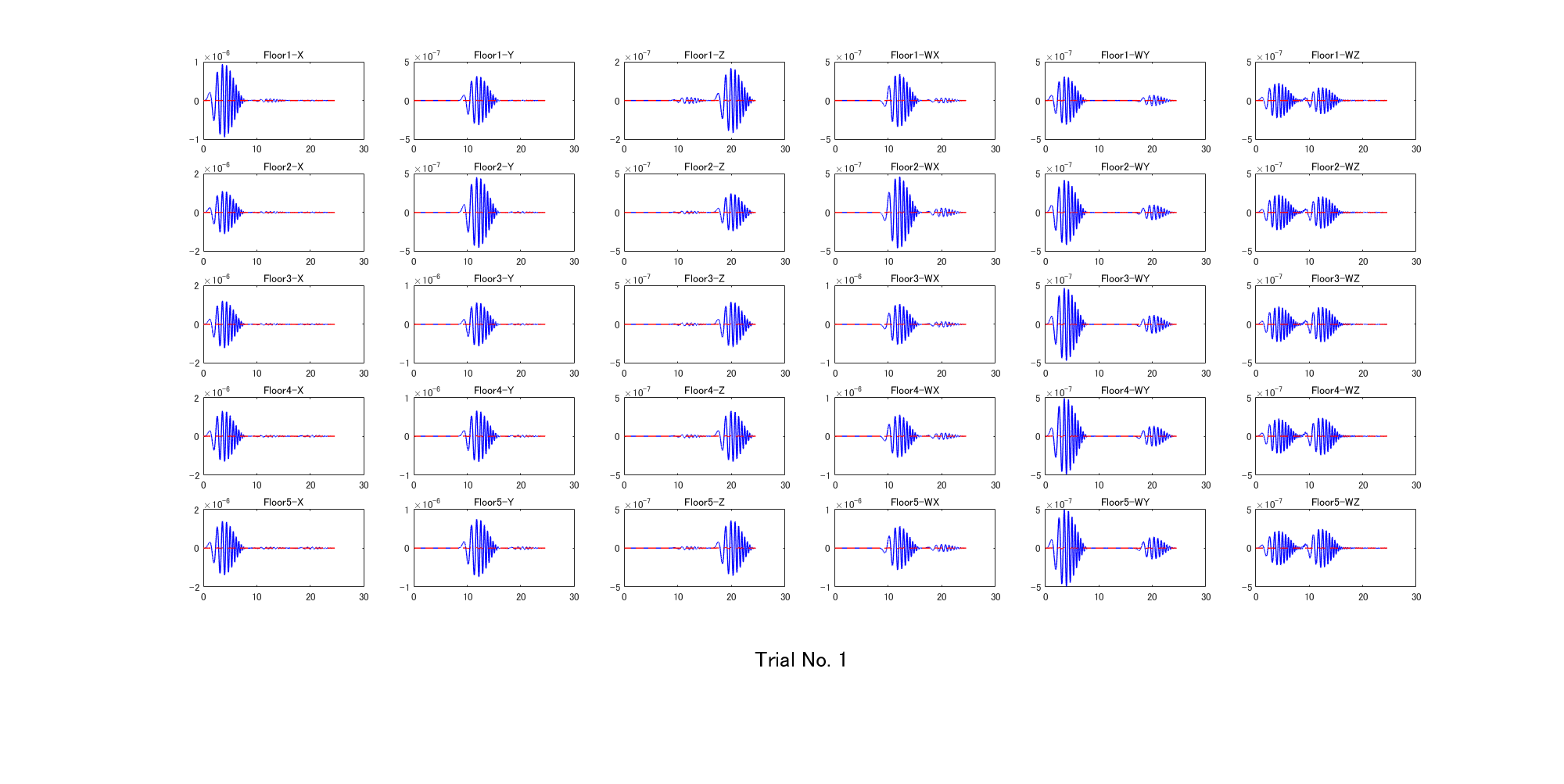
次に,第2回目に試行した結果を下図に示します.wz以外は,概ね実験値に近い波形が得られています.
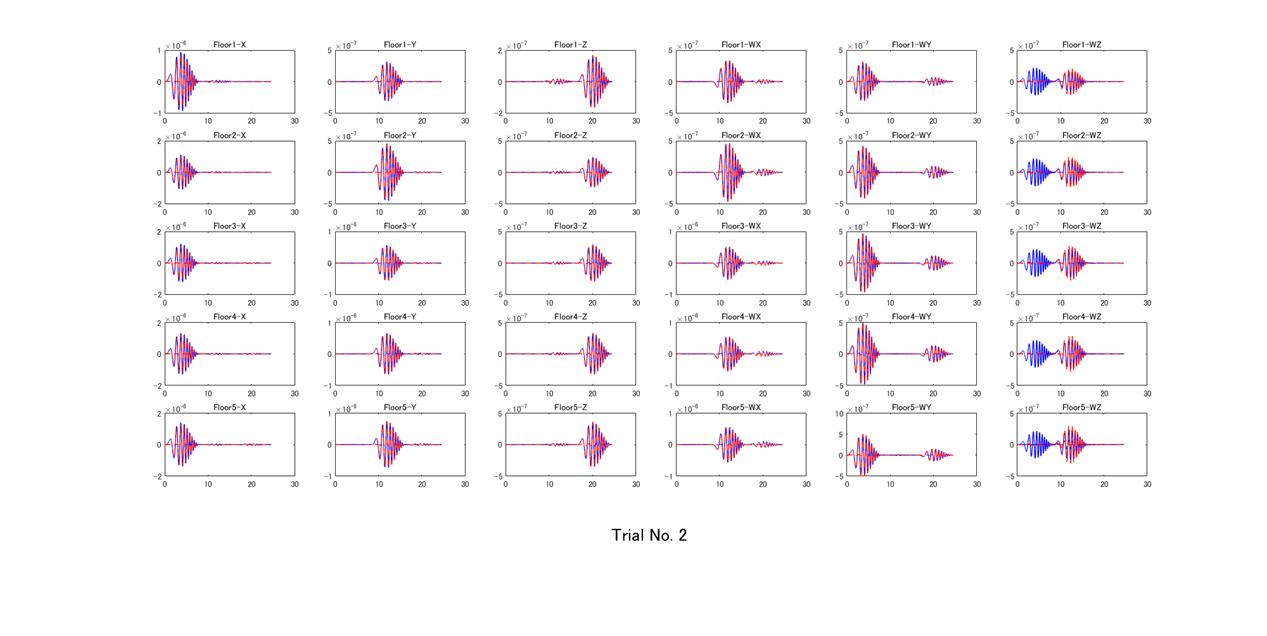
少し飛ばして,第6回目に試行した結果を下図に示します.同定結果(赤線)と真のモデルの結果(青線)は,wzも含めよく一致しています.
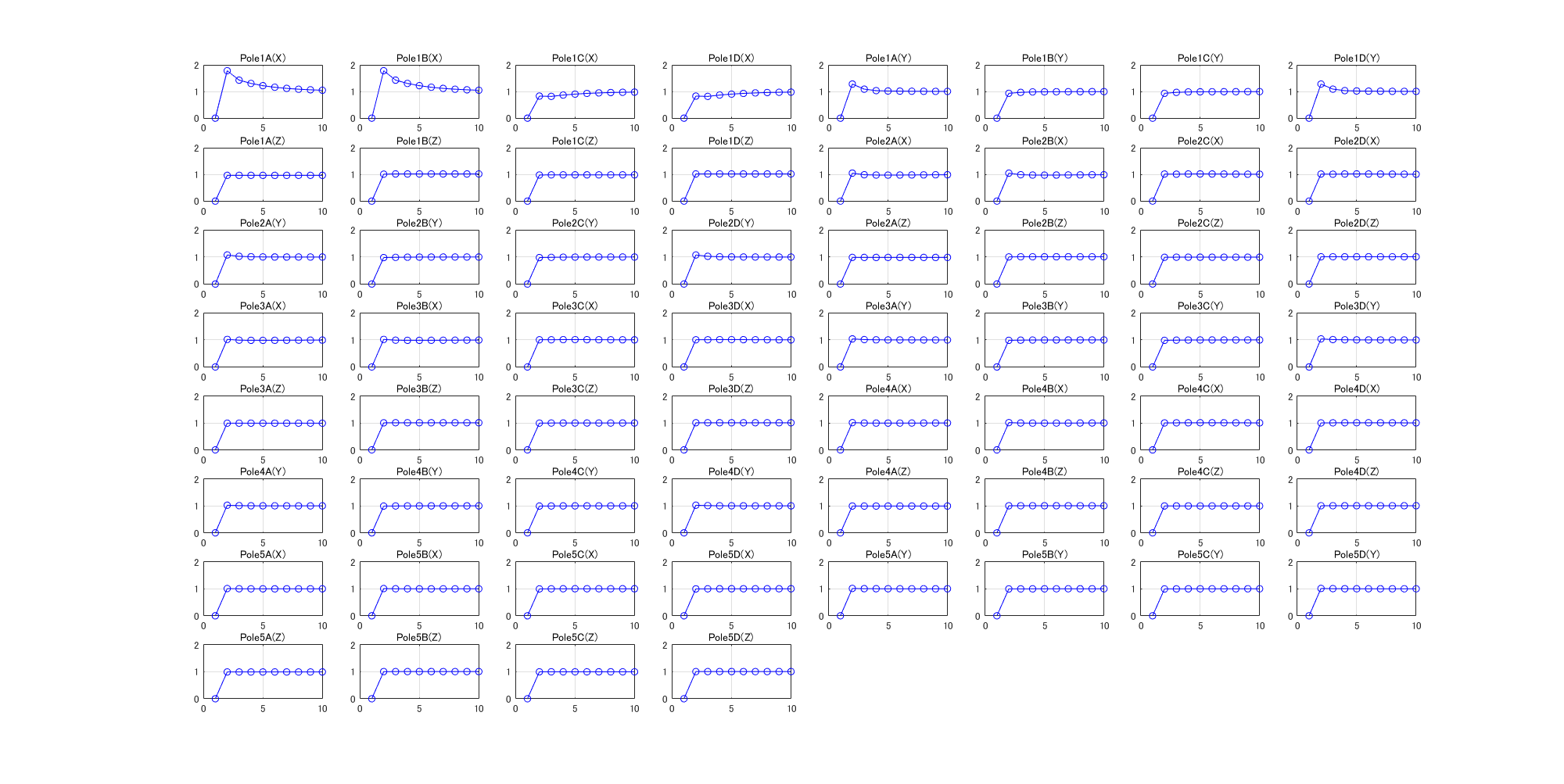
下に示す60個の図は,縦軸が各剛性の真値を同定値で除した同定評価値で,横軸は試行回数です.いずれの図も最初の同定評価値はほぼ零ですが, 試行回数が増えるにしたがって,緩やかに安定的に1へ近づいており,この同定方法が優れていることが分かります. なお,計測ノイズが多くなると,収束結果(精度)は悪くなりますが,収束の安定性は維持されますので,実用上は問題ありません.
ただし,この同定技術は作用点や重心の位置までは同定していません.質量や慣性モーメントは事前の設計情報で十分正確なことが多いので問題は少ないですし,どうしても正確な情報が必要であれば,実験で正確に計測する方法を提供している 企業もあります.
