その他の技術

知的計測技術

　“知的計測”は数学利用が効果を発揮する分野の１つです．ソフト的な方法で「計れないものを計れる」ようにします．コストもかかりません．ときに，手品のように感じて感動する方もいますが，対象を根気よく数式に表現すると，計りたいことを数学的に抽出できる場合があります．ただし，数学力と根気が必要です．コツもあります．
　参考に，知的計測の３つの実績をご紹介します．お悩みの課題に近いようでしたら，ご相談ください．

（１）XYテーブルの経路誤差計測
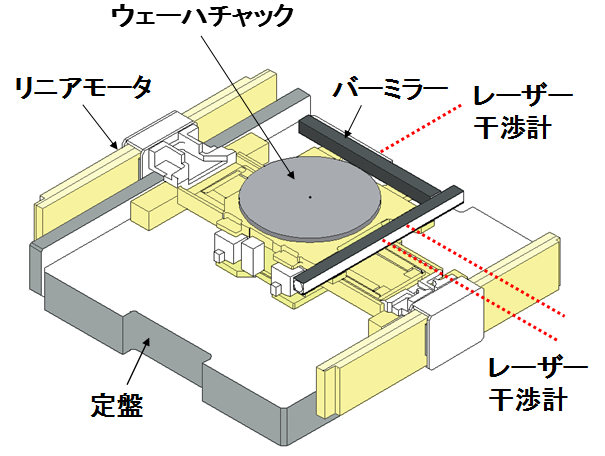　半導体露光装置のXYテーブルは，ナノメートルの位置精度が要求されます．そのため，要求精度で移動経路の真直度を計測する方法がありませんでした．顕微鏡なら精度は十分ですが，測れる範囲が小さすぎます．レーザー干渉計ならば真環境下で広い範囲を計測できますが，費用がかかりすぎます．
　昔は，ウェーハ上にテスト用の重ね合わせマークを露光転写し，隣接するショットで雌雄マークを重ね，そのずれの大きさで評価していました．しかし，それでは移動経路の真直度を計れていません．真直度の差分値を計っているだけです．
　そこで，数学を使いました．移動経路のずれを未知数として雌雄マークのずれを数式で表しました．マークのずれの数だけ方程式ができるので，約1000行の巨大な連立方程式になります．普通はここでやめます．暇じゃないからです．でも数学屋の私は，巨大な連立方程式でも自動的に生成できるプログラムを作りました．計測方法の評価では，敢えて各ショットに位置ずれを与えた露光シミュレーションを行い，その結果から，与えたずれ量を正確に暴きだせるか？確認しました． 詳細な内容はこちら

（２）定盤の微小変形計測
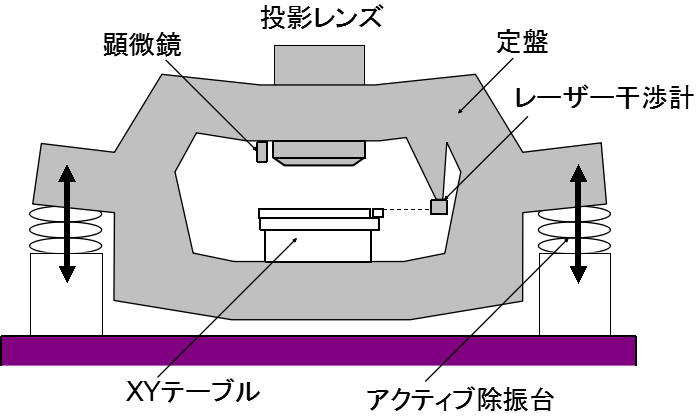　これも半導体露光装置関連です．この装置は数十キロのXYテーブルを10Gほどの棲ざましい加速度で移動させても，位置の繰り返し再現性はナノメートルレベルという，普通では考えられないことを実現しています．もちろん，そのための技術導入も半端じゃありませんし，お値段も高いわけです．投影レンズや位置計測定器を固定する定盤も物凄く頑丈で重い．ところが，XYテーブルが移動するとナノメートルレベルの位置誤差を生じていました．原因は，除振台支持力のバランス変動でした．この原因を突き止めるため，定盤微小変形による位置誤差を計測しました．テーブルの移動経路を変え，定盤変形の異なる状態で雌雄マークを重ね合わせることで，除振台支持力から位置誤差を計測補正する方法を確立しました．本来はダイナミックな現象ですが，静止に近い周波数帯域が大半を占めていたので，静的な問題として扱っても問題はありませんでした．
　こうした方法は思いつきや閃きで導かれるものではありません．誤差を微分方程式で表し，変数として含まれた定盤変形誤差を数学的に抽出することで可能になるのです． 詳細な内容はこちら

（３）誤差の分散分析
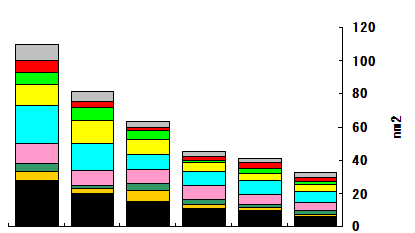　半導体露光装置には精度関連の品質検査データが数多くありますが，以前は合否判定だけに使用していました．（勿体ないことです）そこで，重ね合せ精度のデータを自動的に分析するシステムを開発しました．計測と言うよりデータ解析ですが，見えなかったものを見えるようにしたので，広い意味で計測と言っても差し支えないでしょう．
　ここでは，誤差データだけでなく，データの属性情報（どのウェーハの，どのショットの，どのマークといった情報）とショットやマークの位置情報も併せてセットにしました．そして，誤差の2乗和を属性情報と位置情報で細かく分類しました．シフト成分が20%，回転成分が10%という具合に色分けしました．こうすると，誤差の原因を定量的に把握できます．データを蓄積すると色々なことが分かってきます．原因の見当もつきやすくなります．ここで利用したのは，分散分析と直交回帰分析という統計学の方法です．基礎的な統計手法ですが，単なる手順として覚えている人では応用できません．数学的に統計学を理解していないと応用できないのです． 詳細な内容はこちら

最適化技術

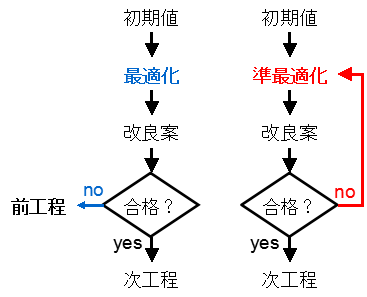　“最適”という言葉は魅力的です．文句の付けようがありません．しかし，実際には合格レベルに達していれば良いものです．時間の許す範囲で複数の候補を比較し，合格するものが現れたら，それを採用します．合格するものが複数あったら一番優れているものを選びます．これを“準最適”と言います．
　ところが，要求が厳しくてなかなか合格するものが現れない場合があります．準最適解法ですと試行錯誤を延々と繰り返す事態に陥ります．半導体露光装置の投影レンズ調整は当にそれでした．出来が悪ければ前工程に戻すしかありませんが，絶対に無理だと分からない限り，諦めがつきません．
　こういうときに真の最適解法が必要になります．最適解でも不合格ならば諦めがつきます．問答無用で前工程に差し戻しです．このとき，数理計画法（線形計画とか整数計画とか言う方法）が役に立ちます．日本の大学には優秀な先生方がいらっしゃるので，躊躇なく相談するべきです．ただし，相談する側に数学的素養は必要です．素養がないと「先生，何とかお願いします」と言って丸投げしようとするでしょう．しかし，先生方は現場のことが分かりません．最悪，仕事の押し付け合いみたいな状況に陥いる場合があるようです．
　一方，企業側に数学屋がいれば，先生の指導を現場で反映できるので，仕事はスムースに進み，次々と成果が現れます．信頼関係が生まれ，関係する人は仕事が楽しくなり，現場の技術者も進んで学ぶようになります．実践によって数理計画法の知識も身につき，最後は現場だけで改良できるようになります．これは実際に経験したことですが，見事な産学連携だったと思います．
　数学屋ほん舗では，真の最適解法に拘ります．数理計画法であれば専門家をご紹介します．それ以外の方法であれば，最適化のコツを身に付けた私共が引き受けます．
　それ以外の方法と言うのは，例えば有効チップ数の最大化です．詳しいことはリンク先のwebページに書いてありますが，簡単に申しますと，無限あるいは膨大な数の候補の中から，最適解の必要条件に一致する候補を選び出して絞り込んでゆきます．そして，十分に絞り込めたら，その中から一番良いものを選ぶのです．ポイントは，最適解の必要条件を見い出すことです．これがコツに相当します．一言で申しますと，それを外すと必ず悪くなってしまうような条件です．そのような条件を数式で表現できれば，最適化はそれほど難しくありません．
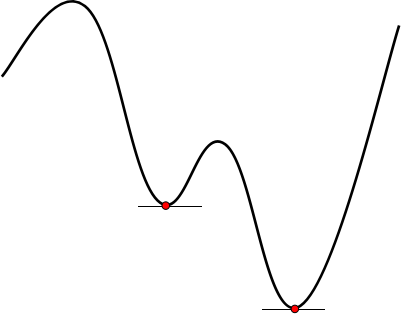
最も良く知られた例に最小２乗法があります．これは，２乗和を評価関数として表して谷を抽出します．こうすることで候補が無限にあった連続領域から，有限個の候補に絞り込んでいます．谷のところでずれれば必ず上がりますから，最適であることの必要条件を満たしています．この条件を数式で表すと，２乗和を形状係数で微分した１次導関数がゼロで２次導関数が正になることです．実は線形計画法も似たような方法で最適解を導いています．