解決方案的重點
在專利公報(日本專利申請特開No.2003-57843,專利No. 4298571,WO2018-216091)中描述了在該站點上提供的半導體佈局優化和縱橫比優化的解決方案。 如果您對解決方案的細節感興趣,則可能需要看一下它們。 但是有很多公式等等,因此它們不易閱讀。 因此,我想集中討論得出最佳解的要點和解的要點。 這樣,您將看到此解決方案的優點和缺點。
共同點(有限)
 半導體佈局優化和長寬比優化中使用的優化的關鍵是候選解的有限化。
優化意味著從候選解決方案中選擇最佳解決方案。
只要候選解的數量是無限的,就無法找到真正的最優解。
半導體佈局優化和長寬比優化中使用的優化的關鍵是候選解的有限化。
優化意味著從候選解決方案中選擇最佳解決方案。
只要候選解的數量是無限的,就無法找到真正的最優解。
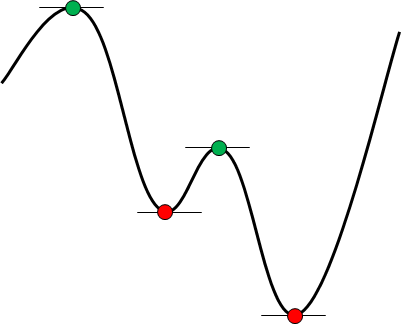
但是,如果候選解是有限的,則有可能在很長一段時間內選擇最佳解。 繪製右圖以顯示有限化示例。 我想從這條曲線中找到最小值。
在這種情況下,曲線的長度是有限的,但是曲線上的點是無限的,因為曲線是連續的。 換句話說,如果您沒有條件搜索,則次數將是無限的。 但是,由於一階導數為零,因此候選解的範圍縮小為四個點,紅色和綠色。 此外,如果加上二階導數為正的條件,則從一開始將是紅色的兩個點。 這是有限化。 如果將其設為有限,則無需將其與無窮大進行比較,因此總會找到最佳解決方案。 這種有限化是獲得最佳解決方案的關鍵。
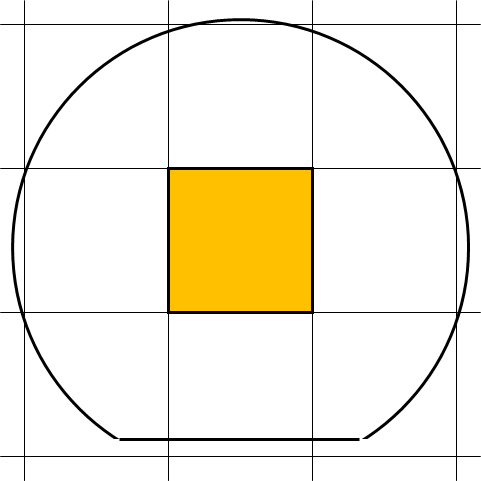 因此,請考慮右圖所示的示例。
在這種情況下,只有一個活動芯片(黃色)。
但是,向上移動晶片會使有效芯片數增加到兩個。
如果左右移動,有效籌碼數將變為三。
大膽地,如果晶片的中心重疊在芯片網格點上,則數量將增加到四個,有效芯片的數量將是四個。
因此,請考慮右圖所示的示例。
在這種情況下,只有一個活動芯片(黃色)。
但是,向上移動晶片會使有效芯片數增加到兩個。
如果左右移動,有效籌碼數將變為三。
大膽地,如果晶片的中心重疊在芯片網格點上,則數量將增加到四個,有效芯片的數量將是四個。
換句話說,一個芯片被分成多個區域,其中有效芯片的數量不同。 順便說一句,在有效籌碼數量增加或減少的邊界上發生了什麼?在那裡,晶片邊界線和芯片晶格點相交。 有效芯片數的增加是由於越過晶片邊界的芯片晶格點移動到晶片內部成為有效芯片,反之,有效芯片數的減少意味著芯片晶格點移動到晶片邊界之外。 意味著它不再是有效的芯片。
現在,讓我們用晶圓邊界上的一個芯片網格點平移晶圓。 然後,另一個芯片晶格點越過晶片邊界線。 如果柵格點在晶片邊界的外部相交並進入晶片邊界的內部,則有效芯片數會增加。 相反,它將減少。
這裡重要的是,當兩個芯片網格點位於晶片邊界上時,它們處於用於計算有效芯片數的理想位置,這是有效芯片數增加和減少的邊界。 換句話說,在兩個芯片網格點在晶片邊界上的條件下,候選解可以是有限的。
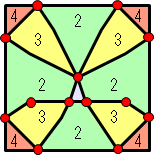 現在,讓我們展示兩個芯片網格點越過晶圓邊界時晶圓中心的位置。
然後,右圖中顯示了13個紅點。
通過將晶圓中心放在這13個點來計算有效芯片的數量。
您可以獲得最大數量的有效芯片和至少一種解決方案。
但是,無法獲得最佳解決方案。
右側圖中彩色的多個區域表示有效籌碼數量相同的區域。
裡面畫的數字表示有效籌碼數。
換句話說,具有四個有效芯片的區域的中心是晶片放置的最佳解決方案。
在圖中,看起來好像有四個部分。
但是,鑑於它是連續圖形的一部分,因此很明顯,最佳解決方案是芯片的角落。
但是,尖端的角不包括在13個紅點中。
現在,讓我們展示兩個芯片網格點越過晶圓邊界時晶圓中心的位置。
然後,右圖中顯示了13個紅點。
通過將晶圓中心放在這13個點來計算有效芯片的數量。
您可以獲得最大數量的有效芯片和至少一種解決方案。
但是,無法獲得最佳解決方案。
右側圖中彩色的多個區域表示有效籌碼數量相同的區域。
裡面畫的數字表示有效籌碼數。
換句話說,具有四個有效芯片的區域的中心是晶片放置的最佳解決方案。
在圖中,看起來好像有四個部分。
但是,鑑於它是連續圖形的一部分,因此很明顯,最佳解決方案是芯片的角落。
但是,尖端的角不包括在13個紅點中。
順便說一句,如右圖所示,如何為每個有效芯片數繪製一個區域圖。 這種解釋非常複雜。 此外,它將與專利和論文相同,因此在此不再贅述。 但是,讓我們只寫結論。 在晶片網格點上覆蓋晶片中心。 接下來,切出穿過晶片邊界線的芯片。 然後,它們全部重疊並通透。 然後,按照右圖創建根據有效籌碼數量的分佈圖。
長寬比優化的要點
 長寬比優化是一個三自由度優化問題,它為晶片放置增加了兩個自由度,為芯片長寬比增加了一個自由度。
要呈現的優化信息是與芯片縱橫比相對應的佈局優化時有效芯片的最大數量。
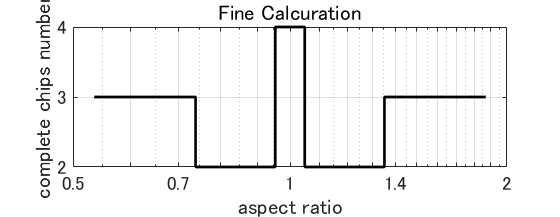
如果以圖形顯示,則水平軸為芯片長寬比,垂直軸為用於放置優化的有效芯片數。
長寬比優化是一個三自由度優化問題,它為晶片放置增加了兩個自由度,為芯片長寬比增加了一個自由度。
要呈現的優化信息是與芯片縱橫比相對應的佈局優化時有效芯片的最大數量。
如果以圖形顯示,則水平軸為芯片長寬比,垂直軸為用於放置優化的有效芯片數。
該圖是折線圖。 當長寬比改變時,有效芯片數以特定的長寬比逐步改變。 右圖是一個示例。 從該圖可以看出,知道有效芯片的最大數量變化的縱橫比和那裡的有效芯片的數量就足夠了。 然後,可以獲得縱橫比優化所需的有限數量的候選解。
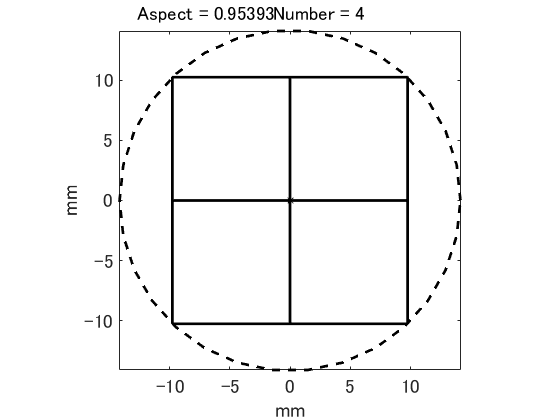 在長寬比優化中,不僅可以調整芯片長寬比,而且可以調整晶片位置的x和y坐標。
在這種情況下,請考慮有效芯片數由於長寬比的變化而增加或減少的現象。
即使調整晶片中心位置,當縱橫比改變為大或小時,有效芯片數也會改變。
在長寬比優化中,不僅可以調整芯片長寬比,而且可以調整晶片位置的x和y坐標。
在這種情況下,請考慮有效芯片數由於長寬比的變化而增加或減少的現象。
即使調整晶片中心位置,當縱橫比改變為大或小時,有效芯片數也會改變。
在這種情況下,多個芯片網格點應位於晶圓邊界圓上。 那麼晶片邊界圓上有多少個芯片晶格點? 對於最多兩個芯片,即使改變芯片的長寬比,也可以保持與晶片邊界圓的接觸狀態。 即使有三個,如果晶片的中心不包含在由這三個點組成的三角形中,那似乎也可以。 但這是極限。 當至少三個芯片柵格點與晶片邊界線相交並且晶片的中心被包括在連接這些交叉點的多邊形內時,縱橫比的變化將增加或減少有效芯片的數量。 例如,在右上圖的情況下。
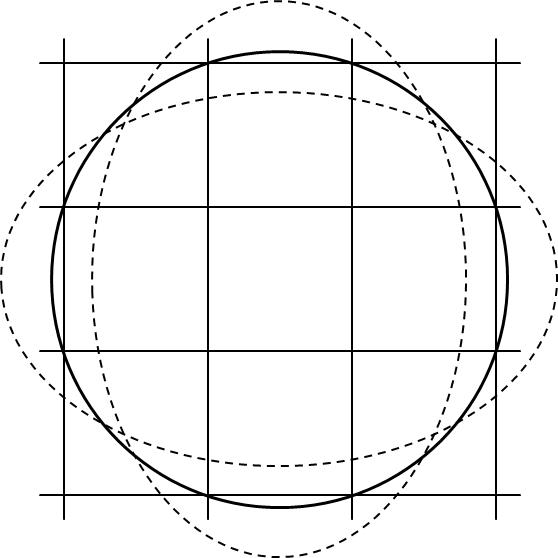 芯片長寬比優化中有限數量的候選解決方案是找到滿足該條件的晶片中心位置和長寬比。
在佈局優化中,我們尋找了兩個芯片網格點接觸晶圓邊界的情況。
同樣,長寬比優化會尋找三個接觸晶片邊界的芯片晶格點。
與佈局優化的不同之處在於,還添加了將晶片的中心包括在連接網格點的三角形(包括側面)內的條件。
芯片長寬比優化中有限數量的候選解決方案是找到滿足該條件的晶片中心位置和長寬比。
在佈局優化中,我們尋找了兩個芯片網格點接觸晶圓邊界的情況。
同樣,長寬比優化會尋找三個接觸晶片邊界的芯片晶格點。
與佈局優化的不同之處在於,還添加了將晶片的中心包括在連接網格點的三角形(包括側面)內的條件。
但是,您在這裡註意到另一個問題。 更改縱橫比會更改每個網格點的位置。 移動量與距晶片邊界圓心的距離成正比。 在佈局優化中,芯片晶格點不會移動,因此我們只需要優化晶片中心位置即可。 但是這次,我無法提出解決方案算法。
因此,我們考慮了一種無需更改芯片網格即可解決的方法。 代替改變芯片網格,它改變了晶片邊界圓的縱橫比。 換句話說,將晶片邊界圓做成橢圓形。 然後,對其進行平移,使其接觸三個選定的網格點。 該方程式求解二次方程組,其中橢圓的長軸和短軸之比和橢圓中心的二維坐標是未知的。 實際上,晶片不能自由變形。 但是,作為一個問題,它被轉換為等效的數學表達式並求解,然後反過來轉換為正確的解。