솔루션의 요점
본 사이트에서 제공하는 반도체 배치 최적화 및 종횡비 최적화의 해법은 특허 공보 (일본 특허 공개 2003-57843 특허 4298571, WO2018-216091)에 적혀 있습니다. 솔루션에 대한 자세한 관심이있는 분은 그들을 참조하십시오. 그러나 특허 공보 수식 등이 많이 쓰여져 있기 때문에 가독성이 없습니다. 그래서 여기에 최적의 솔루션을 이끌 기위한 착안점과 해법의 요점을 설명합니다. 그렇게함으로써이 솔루션의 강점과 약점을 이해할 수 있다고 생각합니다.
공통점 (유한)
 반도체 배치 최적화도 종횡비 최적화도 함께 사용하는 최적화의 기초는 후보 솔루션의 유한 화입니다.
최적화는 후보 솔루션 중에서 가장 좋은 것을 선택하는 것입니다.
만약 후보 해가 무한하고 진정한 최적의 솔루션을 요구하지 않습니다.
반도체 배치 최적화도 종횡비 최적화도 함께 사용하는 최적화의 기초는 후보 솔루션의 유한 화입니다.
최적화는 후보 솔루션 중에서 가장 좋은 것을 선택하는 것입니다.
만약 후보 해가 무한하고 진정한 최적의 솔루션을 요구하지 않습니다.
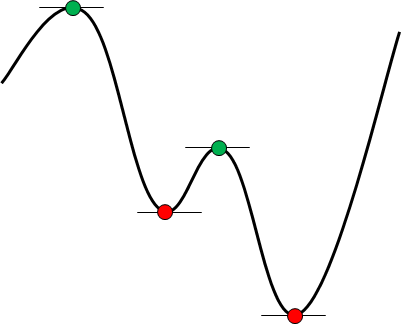
그러나 후보 해석이 유한하다면 반드시 최적의 솔루션을 선택할 수있다합니다. 오른쪽 그림은 유한 화의 일례를 나타 내기 위해 그린 것입니다. 그러면,이 곡선의 최소값을 구합니다.
이 경우, 곡선의 길이는 유한이지만 곡선은 연속이기 때문에, 곡선상의 점은 무한하게 존재하고 있습니다. 즉, 아무것도 조건을 붙이지 않고 탐색하면 그 횟수는 무한 회가되어 버립니다. 그러나 1 차 도함수가 0으로되는 위치를 기준으로하면, 그 후보 해답은 빨간색과 초록색의 4 점으로 좁혀집니다. 또한 2 차 도함수가 긍정적 인 조건도 추가하면 처음부터 빨간색 2 점입니다. 이것이 유한 화입니다. 유한 해지면 무한 비해 필요하지 않으므로 반드시 최적해를 찾을 수 있습니다. 이 유한 화가 최적 해법의 요점입니다.
웨이퍼 배치 최적화의 요점
 "후보 솔루션의 유한 화가 최적 해법의 요점이다"것은, 이해하실 것으로 생각합니다.
그러면, 웨이퍼 배치의 최적 해법을 생각해보십시오.
만약 후보 해가 무한히 있다면 어떻게 할 것인가?
"후보 솔루션의 유한 화가 최적 해법의 요점이다"것은, 이해하실 것으로 생각합니다.
그러면, 웨이퍼 배치의 최적 해법을 생각해보십시오.
만약 후보 해가 무한히 있다면 어떻게 할 것인가?
아마 칩에 다수의 후보 점을 웨이퍼 중심을 배치하고 유효한 칩을 세어 보는 것입니다. 예를 들어, 오른쪽 그림과 같이 후보 지점을 일정한 간격으로 분포시키는 것이 아닐까요? 왜냐하면 간격을 좁게하여 후보 해 점수를 많이할수록 좋은 답을 기대할 수 있기 때문입니다. 그러나 무한 점수를 늘려도 진정 최적 인 것은 모릅니다. 그것은 해가 존재하는 영역이 점이 아니라면이며, 후보 해가 무한히 존재하기 때문입니다. /div>
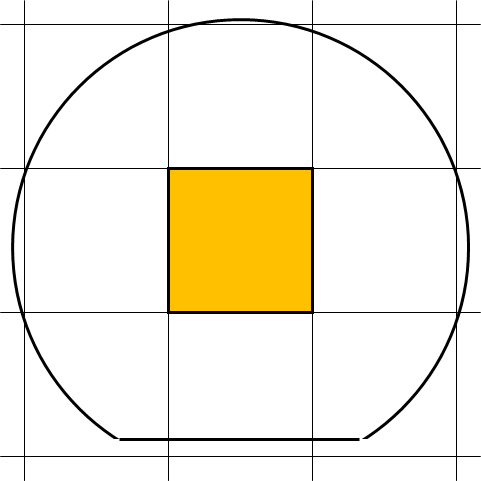 그래서 오른쪽 그림과 같은 예를 생각합니다.
이 경우 유효한 칩 (노란색)는 불과 1 개뿐입니다.
그러나 약간만 웨이퍼를 이동하면 유효 칩의 수는 2 개로 늘어납니다.
또한 좌우로 이동하면 유효 칩의 수는 3 개입니다.
웨이퍼 중심을 칩 격자 점에 거듭하면 유효 칩의 수는 4 개입니다.
그래서 오른쪽 그림과 같은 예를 생각합니다.
이 경우 유효한 칩 (노란색)는 불과 1 개뿐입니다.
그러나 약간만 웨이퍼를 이동하면 유효 칩의 수는 2 개로 늘어납니다.
또한 좌우로 이동하면 유효 칩의 수는 3 개입니다.
웨이퍼 중심을 칩 격자 점에 거듭하면 유효 칩의 수는 4 개입니다.
즉, 하나의 칩은 유효 칩 개수가 다른 여러 영역으로 나눌 수 있습니다. 그런데, 유효 칩의 수를 증감 할 때, 도대체 무엇이 일어나고있는 것일까 요? 거기에서는 웨이퍼 테두리와 칩 격자 점이 교제합니다. 유효 칩 수가 증가하면 웨이퍼 테두리와 어우러진 칩 격자 점이 웨이퍼 내부로 이동합니다. 반대로, 유효 칩의 수가 줄어들 때에는 그 칩 격자 점이 웨이퍼 테두리 밖으로 이동합니다.
그런데 하나의 칩 격자 점이 웨이퍼 경계 선상에있는 상태에서 웨이퍼를 평행 이동시켜 보자. 그러면 다른 칩 격자 점도 웨이퍼 경계와 교차하는 상태가 방문합니다. 웨이퍼 경계의 외측에 있던 격자 점이 교차 한 후 웨이퍼 테두리 안쪽에 들어가면 유효 칩 수가 증가합니다. 그 반대이면 감소하게됩니다.
여기에서 중요한 것은 두 칩 격자 점이 웨이퍼 경계에있을 때 유효한 칩 수가 증감 경계에있는 것입니다. 즉, 2 개의 칩 격자 점이 웨이퍼 경계 선상에있는 조건을 이용하면, 후보 해석을 유한 할 수있는 것입니다.
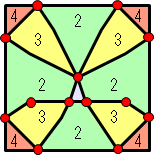 그런데, 2 개의 칩 격자 점이 웨이퍼 경계와 교차 할 때, 웨이퍼 중심의 위치를 표시합시다.
그러면 오른쪽 그림과 13 개의 붉은 점입니다.
이 13 개의 점 웨이퍼 중심을두고 유효 칩 개수를 세어 보아요.
유효 칩의 최대 값과 그것을 실현하는 하나의 솔루션을 얻을 수 있습니다.
그러나 최적의 솔루션을 제공하지는 않습니다.
오른쪽 그림에서 색으로 구분 된 여러 영역은 유효 칩 개수가 동일한 영역을 의미합니다.
그리고 그 안에 그려진 숫자는 유효 칩 수를 보여줍니다.
즉, 유효 칩 수가 4 개 영역의 중심이 웨이퍼 배치의 최적의 솔루션입니다.
그림은 4 곳으로 나뉘어있는 것처럼 생각합니다.
그러나 연속 도형의 일부임을 감안할 때, 최적의 솔루션은 칩의 모서리 인 것은 분명하다.
그러나 칩의 모서리는 13 개의 빨간 점에 포함되지 않습니다.
그런데, 2 개의 칩 격자 점이 웨이퍼 경계와 교차 할 때, 웨이퍼 중심의 위치를 표시합시다.
그러면 오른쪽 그림과 13 개의 붉은 점입니다.
이 13 개의 점 웨이퍼 중심을두고 유효 칩 개수를 세어 보아요.
유효 칩의 최대 값과 그것을 실현하는 하나의 솔루션을 얻을 수 있습니다.
그러나 최적의 솔루션을 제공하지는 않습니다.
오른쪽 그림에서 색으로 구분 된 여러 영역은 유효 칩 개수가 동일한 영역을 의미합니다.
그리고 그 안에 그려진 숫자는 유효 칩 수를 보여줍니다.
즉, 유효 칩 수가 4 개 영역의 중심이 웨이퍼 배치의 최적의 솔루션입니다.
그림은 4 곳으로 나뉘어있는 것처럼 생각합니다.
그러나 연속 도형의 일부임을 감안할 때, 최적의 솔루션은 칩의 모서리 인 것은 분명하다.
그러나 칩의 모서리는 13 개의 빨간 점에 포함되지 않습니다.
그런데 오른쪽 그림과 같은 유효 칩 개수마다의 영역도를 그리려면 어떻게해야할까요. 이 설명은 꽤 복잡합니다. 또한, 특허와 논문과 동일하기 때문에, 여기에서 그만 둡니다. 그러나 결론 만 씁시다. 웨이퍼 중심을 칩 격자 점에 거듭합니다. 다음으로, 웨이퍼 테두리가 통과하는 칩을 잘라냅니다. 그리고 그들 모두를 거듭 투시하는 것입니다. 그러면 오른쪽 그림과 같은 유효 칩 개수 별 분포도 수 있습니다.
칩 종횡비 최적화의 핵심 사항
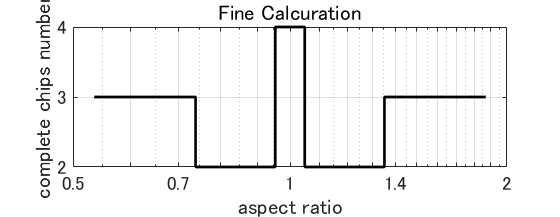 종횡비 최적화는 웨이퍼 배치의 2 자유와 칩 종횡비 1 자유도를 더한 3 자유도의 최적화 문제입니다.
제시하고자 최적화 정보는 칩 종횡비에 대응하는 배치 최적화시 최대 유효 칩 수 있습니다.
그래프로 표시하는 경우, 가로축이 칩 종횡비, 세로축이 배치 최적화시의 유효 칩 개수입니다.
종횡비 최적화는 웨이퍼 배치의 2 자유와 칩 종횡비 1 자유도를 더한 3 자유도의 최적화 문제입니다.
제시하고자 최적화 정보는 칩 종횡비에 대응하는 배치 최적화시 최대 유효 칩 수 있습니다.
그래프로 표시하는 경우, 가로축이 칩 종횡비, 세로축이 배치 최적화시의 유효 칩 개수입니다.
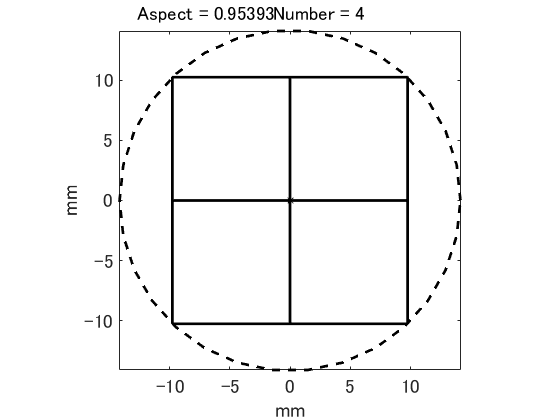
그래프는 선 그래프입니다. 종횡비가 변화하면 특정 비율로 사용 칩 수가 계단 모양으로 변화합니다. 오른쪽 그림은 그 예입니다. 이 그림에서 알 수 있듯이, 최대 유효 칩 수가 변화하는 비율과 거기에서 유효 칩 개수를 알면 충분하다. 그리고 종횡비 최적화에 필요한 후보 솔루션의 유한를 할 수 있습니다.
 종횡비 최적화는 끝 종횡비뿐만 아니라 웨이퍼 위치의 x 및 y 좌표도 조정할 수 있습니다.
그 조건에서 종횡비 변화에 유효한 칩 수가 증감하는 현상을 생각합니다.
웨이퍼 중심 위치를 조정해도 종횡비를 대소 중 하나에 변화 시키면 유효 칩 수가 다를 수 있습니다.
종횡비 최적화는 끝 종횡비뿐만 아니라 웨이퍼 위치의 x 및 y 좌표도 조정할 수 있습니다.
그 조건에서 종횡비 변화에 유효한 칩 수가 증감하는 현상을 생각합니다.
웨이퍼 중심 위치를 조정해도 종횡비를 대소 중 하나에 변화 시키면 유효 칩 수가 다를 수 있습니다.
이런 경우 여러 칩 격자 점이 웨이퍼 경계 엔에 있어야합니다. 그럼 도대체 몇개의 칩 격자 점이 웨이퍼 경계 엔에있는 것입니까? 2 개까지라면 칩 종횡비를 변화 시켜도 웨이퍼 경계 원형에 접촉 한 상태를 유지할 수 있습니다. 3 개라도 그 3 점으로 만드는 삼각형 안의 웨이퍼 중심이 들어가 있지 않으면 괜찮을 것입니다. 그러나 이것이 한계입니다. 칩 격자 점의 적어도 3 점이 웨이퍼 테두리와 어우러져 그 교점을 맺은 다각형의 내부에 웨이퍼 중심이 포함되어있을 때, 종횡비 변화에 유효 칩 수가 증감합니다. 예를 들어, 오른쪽 그림과 같은 경우입니다.
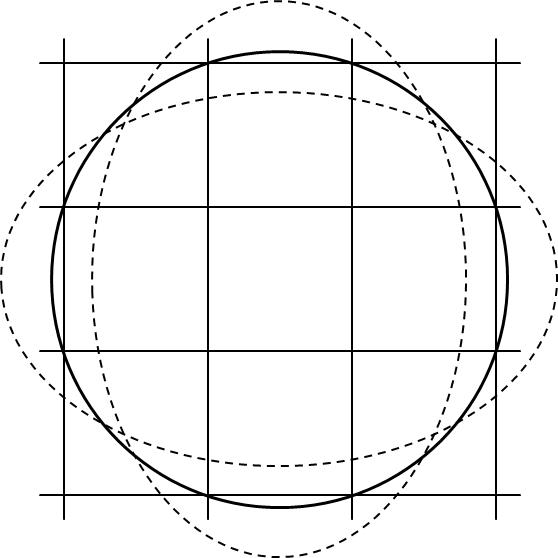 칩 종횡비 최적화의 후보 솔루션의 유한 화는이 조건을 충족 웨이퍼 중심 위치와 비율을 구하는 것입니다.
배치 최적화는 웨이퍼 테두리에 2 개의 칩 격자 점이 접하는 경우를 찾았습니다.
그러나 이번에는 해법 알고리즘을 생각해 없습니다.
칩 종횡비 최적화의 후보 솔루션의 유한 화는이 조건을 충족 웨이퍼 중심 위치와 비율을 구하는 것입니다.
배치 최적화는 웨이퍼 테두리에 2 개의 칩 격자 점이 접하는 경우를 찾았습니다.
그러나 이번에는 해법 알고리즘을 생각해 없습니다.
그래서 칩 격자를 변화시키지 해결 방법을 생각했습니다. 칩 격자를 변화시키지 않는 대신 웨이퍼 경계 원형의 비율을 변화시키는 것입니다. 즉, 웨이퍼 경계 원형을 타원형으로하는 것입니다. 그리고이를 평행 이동시켜, 미리 뽑아 놓은 3 점의 격자 점과 접하게됩니다. 수식에서는 타원의 장축과 단축의 비율과 타원 중심의 2 차원 좌표를 미지수로 한 연립 이차 방정식을 풉니 다. 사실, 웨이퍼를 자유롭게 변형 할 수는 없습니다. 그러나 문제 등가 인 수식 표현으로 변환하여 풀고 다음 역변환하여 올바른 답을합니다.