解决方案的重点
在专利公报(JP2003-57843,JP4298571,WO2018-216091)中描述了在该站点上提供的半导体的布局优化和纵横比优化的解决方案。 如果您对解决方案的详细信息感兴趣,请参阅它们。 但是,专利公报包含许多数学公式,因此不容易阅读。 因此,在这里我们将解释兴趣点和解决方案的关键点,以找到最佳解决方案。 这样,您将了解此解决方案的优点和缺点。
共同点(有限)
 半导体布局优化和长宽比优化中使用的优化的关键是候选解的有限化。
优化是从候选解决方案中选择最佳解决方案。
如果候选解的数量是无限的,则无法找到真正的最优解。
半导体布局优化和长宽比优化中使用的优化的关键是候选解的有限化。
优化是从候选解决方案中选择最佳解决方案。
如果候选解的数量是无限的,则无法找到真正的最优解。
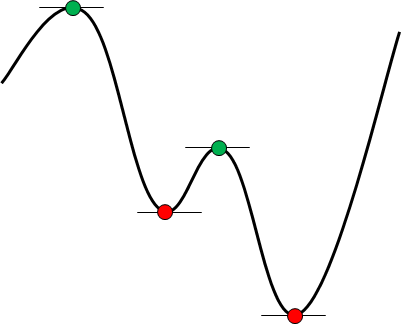
但是,如果候选解是有限的,则可以始终选择最佳解。 绘制右图以显示有限化示例。 然后,从该曲线中找到最小值。
在这种情况下,曲线的长度是有限的,但是曲线是连续的,因此曲线上的点是无限的。 换句话说,如果您没有条件进行搜索,则次数将是无限的。 但是,假定一阶导数为零,则候选解将减少为红色和绿色四个点。 另外,如果我们加上二阶导数为正的条件,它将是从开始算起的红色两点。 这是有限化。 如果将其设为有限,则无需将其与无穷大进行比较,因此总会找到最佳解决方案。 这种有限化是获得最佳解决方案的关键。
展示位置优化的要点
 您可能已经理解“候选解决方案的有限解决方案是最佳解决方案的关键”。
因此,让我们从晶圆放置的最佳解决方案开始。
如果我们不考虑有限的候选解怎么办?
您可能已经理解“候选解决方案的有限解决方案是最佳解决方案的关键”。
因此,让我们从晶圆放置的最佳解决方案开始。
如果我们不考虑有限的候选解怎么办?
也许,如果您在晶片中心的芯片中放置了很多候选点,您将尝试计算有效芯片。 例如,候选点不是如右图所示以相等的间隔分布吗?如果间隔变窄并且候选解决方案的数量增加,则可以期望得到更好的解决方案,但是尚不清楚无论增加多少点,它的确是最优的。 因为解存在的区域不是点而是表面,所以存在无限的候选解。 至少可以找到有效筹码数量的最大值会很好,但是我不知道。 不知何故,我想考虑候选解的有限性,但是如果不多考虑,我就不会考虑它。
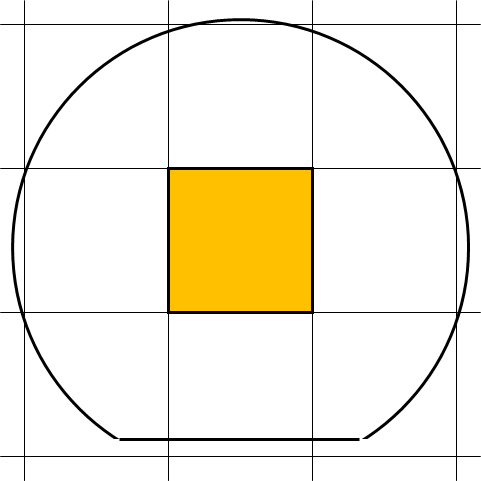 因此,请考虑右图所示的示例。
在这种情况下,只有一个活动芯片(黄色)。
但是,向上移动少量晶片会使有源芯片的数量增加到两个。
如果左右移动,有效筹码数将为三。
大胆地,如果晶片中心叠加在芯片晶格点上,则数量将增加到四个,而有效芯片的数量将是四个。
因此,请考虑右图所示的示例。
在这种情况下,只有一个活动芯片(黄色)。
但是,向上移动少量晶片会使有源芯片的数量增加到两个。
如果左右移动,有效筹码数将为三。
大胆地,如果晶片中心叠加在芯片晶格点上,则数量将增加到四个,而有效芯片的数量将是四个。
现在,让我们用晶圆边界上的一个芯片网格点平移晶圆。 然后,另一个芯片晶格点越过晶片边界线。 如果栅格点在晶片边界的外部相交并进入晶片边界的内部,则有效芯片数会增加。 相反,它将减少。
这里重要的是,当两个芯片网格点在晶圆边界上时,有效芯片数在边界上。 换句话说,通过使用两个芯片网格点在晶片边界上的条件,候选解可以是有限的。
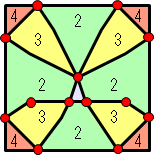 现在,让我们展示两个芯片网格点越过晶圆边界时晶圆中心的位置。
然后,右图中显示了13个红点。
通过将晶圆中心放在这13个点来计算有效芯片的数量。
您可以获得最大数量的有效芯片和至少一种解决方案。
但是,无法获得最佳解决方案。
右侧图中彩色的多个区域表示有效筹码数量相同的区域。
里面画的数字表示有效筹码数。
换句话说,具有四个有效芯片的区域的中心是晶片放置的最佳解决方案。
在图中,看起来好像有四个部分。
但是,鉴于它是连续图形的一部分,因此很明显,最佳解决方案是芯片的角落。
但是,尖端的角不包括在13个红点中。
现在,让我们展示两个芯片网格点越过晶圆边界时晶圆中心的位置。
然后,右图中显示了13个红点。
通过将晶圆中心放在这13个点来计算有效芯片的数量。
您可以获得最大数量的有效芯片和至少一种解决方案。
但是,无法获得最佳解决方案。
右侧图中彩色的多个区域表示有效筹码数量相同的区域。
里面画的数字表示有效筹码数。
换句话说,具有四个有效芯片的区域的中心是晶片放置的最佳解决方案。
在图中,看起来好像有四个部分。
但是,鉴于它是连续图形的一部分,因此很明显,最佳解决方案是芯片的角落。
但是,尖端的角不包括在13个红点中。
长宽比优化的要点
 长宽比优化是一个三自由度优化问题,它为晶片放置增加了两个自由度,为芯片长宽比增加了一个自由度。
要呈现的优化信息是与芯片纵横比相对应的用于布局优化的有效芯片的最大数量。
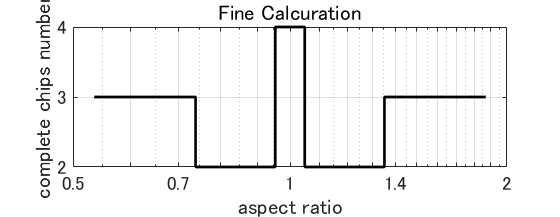
如果将其显示为图形,则水平轴为芯片长宽比,垂直轴为用于布局优化的有效芯片数。
长宽比优化是一个三自由度优化问题,它为晶片放置增加了两个自由度,为芯片长宽比增加了一个自由度。
要呈现的优化信息是与芯片纵横比相对应的用于布局优化的有效芯片的最大数量。
如果将其显示为图形,则水平轴为芯片长宽比,垂直轴为用于布局优化的有效芯片数。
该图是折线图。 当长宽比改变时,有效芯片数以特定的长宽比逐步改变。 右图是一个示例。 从该图可以看出,知道有效芯片的最大数量变化的纵横比和那里的有效芯片的数量就足够了。 然后,可以获得纵横比优化所需的有限数量的候选解。
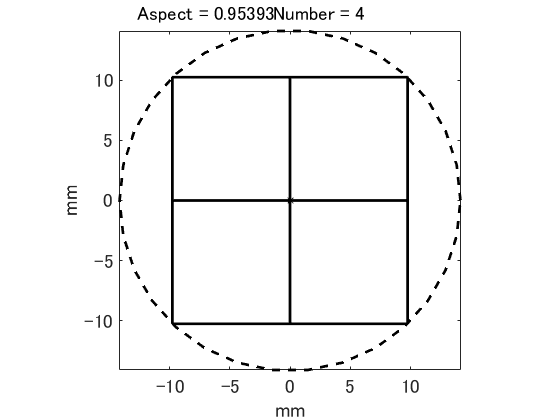 在长宽比优化中,不仅可以调整芯片长宽比,而且可以调整晶片位置的x和y坐标。
在这种情况下,请考虑由于长宽比的变化而导致有效芯片数增加或减少的现象。
即使调整晶片的中心位置,如果纵横比更改为大或小,有效芯片数也会改变。
在长宽比优化中,不仅可以调整芯片长宽比,而且可以调整晶片位置的x和y坐标。
在这种情况下,请考虑由于长宽比的变化而导致有效芯片数增加或减少的现象。
即使调整晶片的中心位置,如果纵横比更改为大或小,有效芯片数也会改变。
在这种情况下,多个芯片网格点应位于晶圆边界圆上。 那么晶片边界圆上有多少个芯片晶格点? 对于最多两个芯片,即使改变芯片的长宽比,也可以保持与晶片边界圆的接触状态。 即使有三个,如果晶片的中心不包含在由这三个点组成的三角形中,那似乎也可以。 但这是极限。 当至少三个芯片栅格点与晶片边界线相交并且晶片的中心被包括在连接这些交点的多边形内时,纵横比的变化将增加或减少有效芯片的数量。 例如,在右上图的情况下。
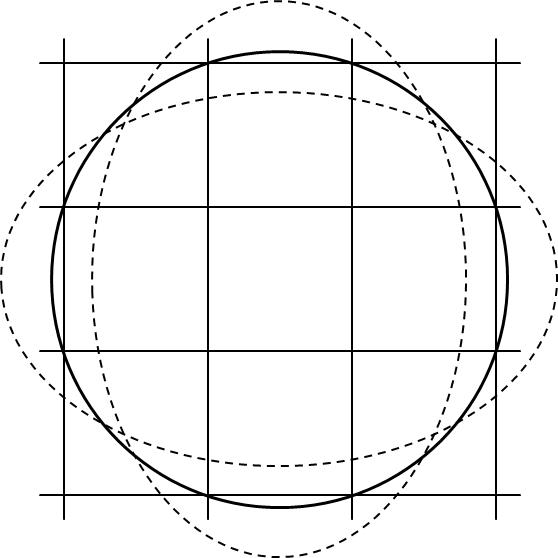 芯片长宽比优化中有限数量的候选解决方案是找到满足该条件的晶片中心位置和长宽比。
在布局优化中,我们寻找了两个芯片网格点接触晶圆边界的情况。
同样,长宽比优化会寻找三个接触晶片边界的芯片晶格点。
与放置优化不同的是,晶片的中心位于连接网格点的三角形内部(包括侧面)。
芯片长宽比优化中有限数量的候选解决方案是找到满足该条件的晶片中心位置和长宽比。
在布局优化中,我们寻找了两个芯片网格点接触晶圆边界的情况。
同样,长宽比优化会寻找三个接触晶片边界的芯片晶格点。
与放置优化不同的是,晶片的中心位于连接网格点的三角形内部(包括侧面)。
但是,您在这里注意到另一个问题。 更改纵横比会更改每个网格点的位置。 移动量与距晶片边界圆心的距离成正比。 在布局优化中,芯片晶格点不会移动,因此我们只需要优化晶片中心位置即可。 但是这次,我无法提出解决方案算法。
因此,我们考虑了一种无需更改芯片网格即可解决的方法。 代替改变芯片网格,它改变了晶片边界圆的纵横比。 换句话说,将晶片边界圆做成椭圆形。 然后,对其进行平移,使其接触三个选定的网格点。 该方程式求解二次方程组,其中椭圆的长轴和短轴之比和椭圆中心的二维坐标是未知的。 实际上,晶片不能自由变形。 但是,作为一个问题,它被转换为等效的数学表达式并求解,然后反过来转换为正确的解。