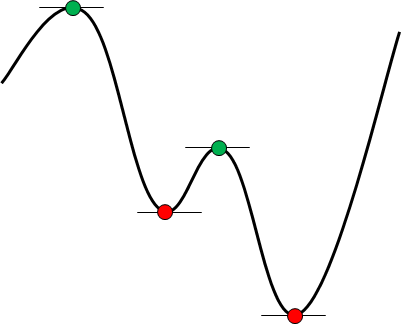
半導体の配置最適化も縦横比最適化も，共に用いている最適化の要点は，候補解の有限化です．最適化と言うのは，候補解の中から一番良いものを選ぶことです．候補解が無限にある限り，真の最適解は求められません．
　しかし，候補解が有限であれば，長い時間をかければ，必ず最適解を選び出すことができます．右の図は，有限化の一例を示すために描いたものです．この曲線の中から最小値を求めようと思います．
　この場合，曲線の長さは有限ですが，曲線は連続ですから，曲線上の点は無限に存在しています．つまり，何も条件を付けずに探索すれば，その回数は無限回になってしまいます．しかし， 1次導関数が零になる位置を条件にすれば，その候補解は赤と緑の4点に絞られます．さらに，2次導関数が正である条件も追加すれば，最初から赤の2点になります．これが，有限化です．有限化すれば，無限に比べなくて済むので，必ず最適解が見つかります．この有限化こそが最適解法のコツなのです．

　「候補解の有限化が最適解法のコツである」と言うことは，もうご理解頂けたと思います．そこで，ウェーハ配置の最適解法から考えてみましょう．もし，候補解の有限化など考えないとすれば，どうするでしょうか？
　多分，チップ内に多数の候補点をウェーハ中心を配置しては，有効チップを数えてみるでしょう．例えば，右図のように候補点を等間隔に分布させるのではないでしょうか？間隔を狭くして，候補解の点数を多くするほど良い解が期待できますが，いくら点数を増やしても真に最適であることは分かりません．それは，解が存在する領域が点ではなくて面だから，候補解が無限に存在するからです．せめて，有効チップ数の最大値だけでも分かれば，良いのですが，それも分かりません．何とか，候補解の有限化を考えたいと思いますが，もう少し，考察しないと思い浮かびそうにありません．

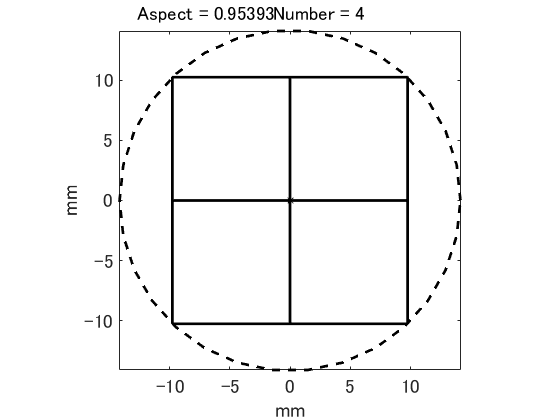
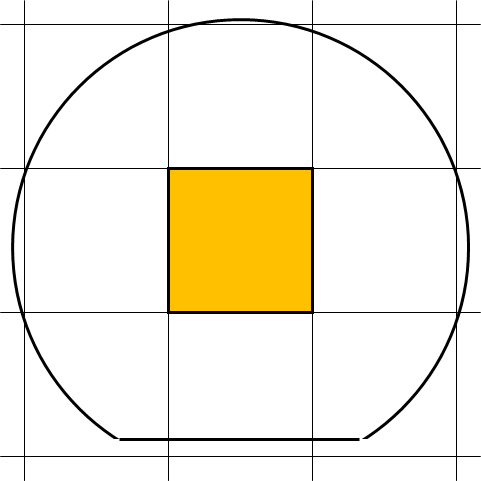　そこで，右図のような例で考えます．この場合，有効チップ（黄色）は僅かに 1個だけです．しかし，ほんの少しだけウェーハを上に移動すれば，有効チップの数は 2個に増えます．さらに，左右に移動すれば有効チップの数は 3個になります．思い切って，ウェーハ中心をチップ格子点に重ねれば，さらに増えて，有効チップの数は 4個になります．
　つまり， 1つのチップは有効チップ数が異なる複数の領域に分割されているのです．ところで，有効チップの数が増減する境界では，いったい何が起きているのでしょうか？　そこでは，ウェーハ境界線とチップ格子点が交わっているのです．有効チップ数が増えるのは，ウェーハ境界線と交わったチップ格子点がウェーハ内部に移動して有効チップになることであり，逆に減るということは，チップ格子点がウェーハ境界線の外に移動して，有効チップでなくなることを意味しています．
　さて， 1つのチップ格子点がウェーハ境界線上にある状態で，ウェーハを平行移動させてゆくと，別のチップ格子点もウェーハ境界線と交差する状態になります．交差する前の格子点がウェーハ境界の外側にあったとすれば，交差して，さらにウェーハ境界線の内側に入れば，有効チップ数は増加し，その逆であれば減少することになります．
　ここで重要なことは， 2つのチップ格子点がウェーハ境界線上にあるときは，有効チップ数が増減する境界という，有効チップ数を数えるには絶好の位置にあるということです．
　つまり， 2つのチップ格子点がウェーハ境界線上にある条件で，候補解を有限化できるのです．

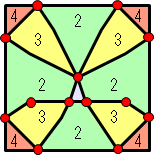　さて， 2つのチップ格子点がウェーハ境界線と交わるとき，ウェーハ中心の位置を示すと，右図に示す 13個の赤点になります．これら 13個の点にウェーハ中心を置いて有効チップ数を数えれば，有効チップ数の最大値とそれを実現する少なくとも 1つの解を得ることができます．しかし，最適解は得られません．右図で色分けされた複数の領域は，有効チップ数が等しい領域を意味しており，その中に描かれた数字は有効チップ数を示しています．つまり，有効チップ数が 4個の領域の中心がウェーハ配置の最適解です．図では， 4か所に別れているように思えますが，連続図形の一部であることを考えれば，最適解はチップの角であることは明らかですが，13個の赤い点には含まれていません．
　ところで，13個の赤い点だけでなく，右図のような有効チップ数毎の領域図を描くにはどうすればよいか？と申しますと，これは結構ややこしい．ここのところを真面目に説明すると，特許や論文と同じになるので，ここではやめておきますが，ただ，理由は抜きに結論だけ書くと，ウェーハ中心をチップ格子点に重ねたとき，ウェーハ境界線が通過するチップを切り出して，それらを全て重ねて透視すると，右図のような有効チップ数別の分布図ができます．

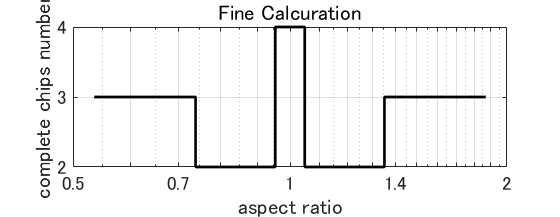　縦横比最適化とは，ウェーハ配置の 2自由度とチップ縦横比の 1自由度を加えた 3自由度の最適化問題です．提示したい最適化情報は，チップ縦横比に対応する配置最適化時の最大有効チップ数になります．グラフで表示するのであれば，横軸がチップ縦横比，縦軸が配置最適化時の有効チップ数となります．
　グラフは，縦横比が変化すると，特定の縦横比で有効チップ数が階段状に変化する折れ線グラフとなります．右図はその一例です．これから分かるように，最大有効チップ数が変化する縦横比とそこでの有効チップ数が分かれば，それ以外の情報は要りません．つまり，この折れ点となる縦横比を突き止めることが，候補解の有限化になるのです．

　さて，縦横比の変化によって，有効チップ数が増減するときの状態を考えます．縦横比最適化と言っても，実際の自由度は縦横比と 2次元のウェーハ位置です．つまり，ウェーハ中心位置をいくら自由に動かしても，縦横比をほんの少し変化させると有効チップ数が変わってしまうということです．
　ところで，有効チップ数が変わる境目というのは，チップ格子点がウェーハ境界円上あるときですが，いったい何個のチップ格子点がウェーハ境界円上にあるのでしょうか？ウェーハ中心位置を自由に動かせるならば， 2個まではチップ縦横比を変化させても，ウェーハ境界円に接触した状態を維持できそうです． 3つでも，その 3点で作る三角形の中にウェーハ中心が入っていなければ，大丈夫そうですが，これが限界です．つまり，縦横比の変化で有効チップ数が増減するときは，チップ格子点の少なくとも 3点がウェーハ境界線と交わり，それらの交点を結んだ多角形の内部にウェーハ中心が含まれていると考えられます．例えば右上図のように，チップ格子点の 4点がウェーハ境界円に接していて，この 4点を円に沿って結んだ多角形の内側にウェーハ境界円の中心が含まれているような場合です．

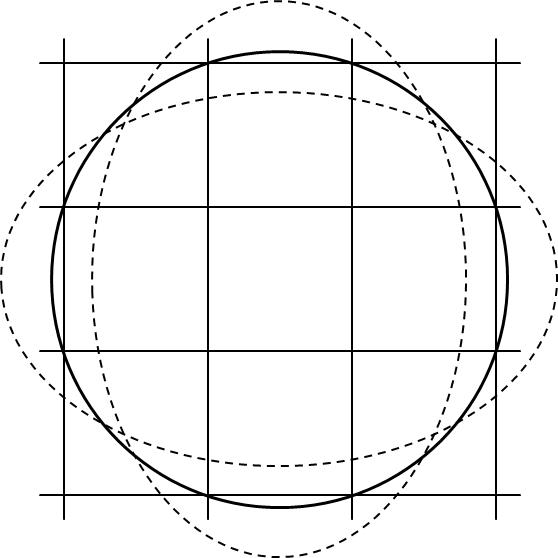　チップ縦横比最適化における候補解の有限化というのは，この条件を満たすウェーハ中心位置と縦横比を求めることになります．それは，配置最適化の場合にウェーハ境界線に 2つのチップ格子点が接する場合を探したのとよく似ています．違うのは，ウェーハ境界線に 3つのチップ格子点が接することと，その 3点を結んだ三角形の内側（辺上も含む）にウェーハ境界円の中心が含まれることの条件を満たすことです．
　ところが，ここに大きな問題があります．縦横比を変化させると，各格子点の位置が変化し，その移動量はウェーハ境界円の中心からの距離に比例します．配置最適化のとき，チップ格子点は移動しませんでしたから，この点は大きな問題になりました．
　そこで，チップ格子を変化させないで解く方法を考えました．チップ格子を変化させない代わりに，ウェーハ境界円の縦横比を変化させるのです．つまり，ウェーハ境界円を楕円にすると同時に平行移動させ，予め選んでおいた3点の格子点と接するように，楕円の長軸と短軸の比率と楕円中心の2次元座標を未知数とする連立2次方程式を解きます．実際には，ウェーハを自由に変形できることはありませんが，問題として等価な数式表現に変換して解き，最後に逆変換して，正しい解にすれば良いのです．