앞으로 반도체 레이아웃을 설계하는 단계에 있다면 " 종횡비 최적화 "를 선택하십시오. 열린 입력 화면에서 6 개의 항목을 설정하십시오.
  ① 웨이퍼 직경
  ② 오리엔테이션 플랫 길이 （제로 용 노치 타입）
  ③ 유효하지 않은 영역 너비
  ④ 칩 면적
  ⑤ 최소 종횡비
  ⑥ 최대 종횡비
① ~ ⑥의 초기 값은 자유롭게 삽입 될 수 있습니다.
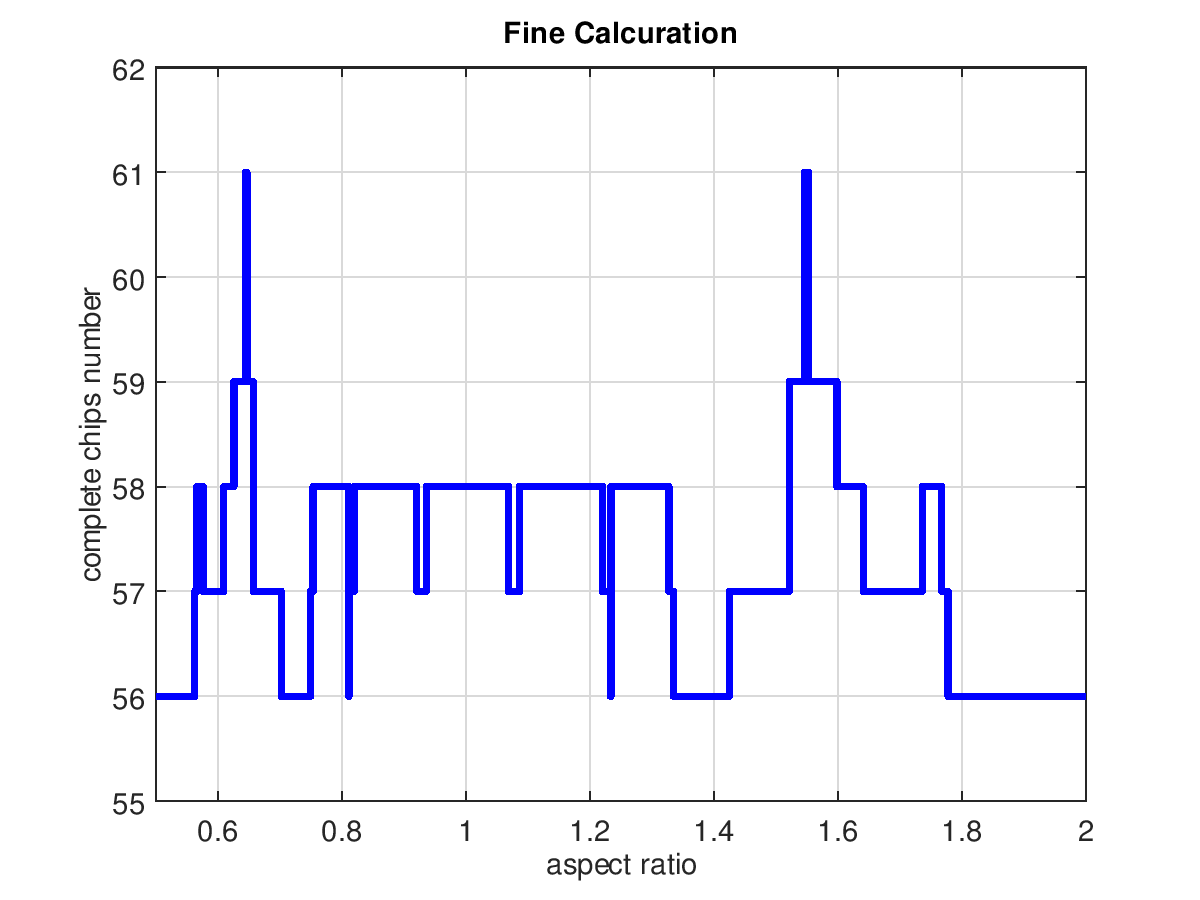
30 초 정도 기다리면 가로축에 칩 종횡비, 세로축 최대 유효 칩 수를 나타내는 오른쪽 그림이 나타납니다.

그런데, 유효 칩 수가 최대 (61 개)가 될 종횡비는 그 범위가 매우 좁고 잘 모르겠습니다. 그래서 종횡비의 상하를 조금씩 좁혀 계산을 반복합니다. 그러자 그 비율이 0.65 부근에있는 것을 알 수 있습니다.
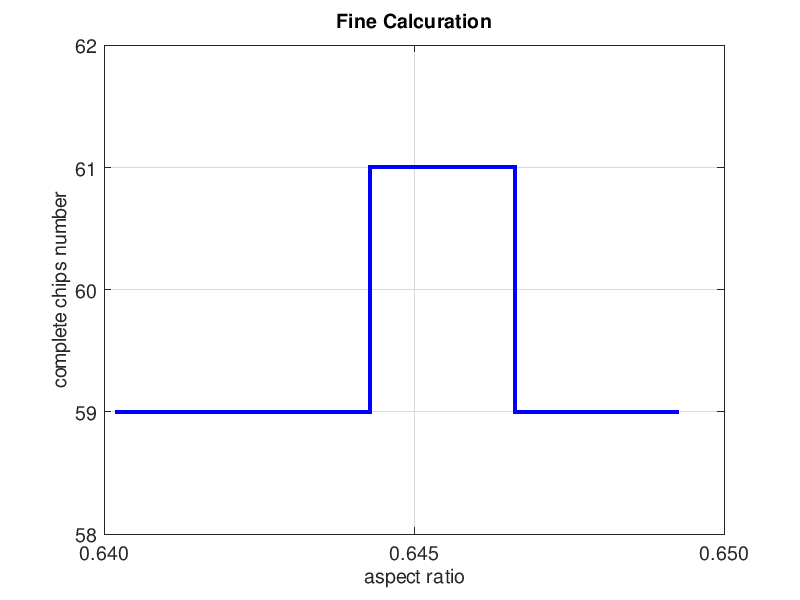
오른쪽 그림은 가로 세로 비율의 범위를 0.64 ~ 0.65로 변경하고 다시 계산 한 결과입니다. 종횡비가 0.645이면 유효 칩 개수는 61 개가 될 것을 알 수 있습니다.

유효 칩 수는 종횡비가 0.645 부근에서 최대가됩니다. 그 형상으로 레이아웃 설계 할 수 있다면, 거기에 넘었던 적은 없습니다.
그러나 그것이 무리라면 유효 칩 수가 많은 다른 종횡비를 선택합니다. 그러나 여기서 끝해서는 없습니다. 드물게입니다 만, 계산 오차로 인해 종횡비와 유효 칩 개수의 관계도에 오류가 발생합니다. 따라서 종횡비와 유효 칩 개수의 관계도를 그대로 받아들이지 않고 배치 최적화를 사용하여 유효 칩 개수를 확인합니다.
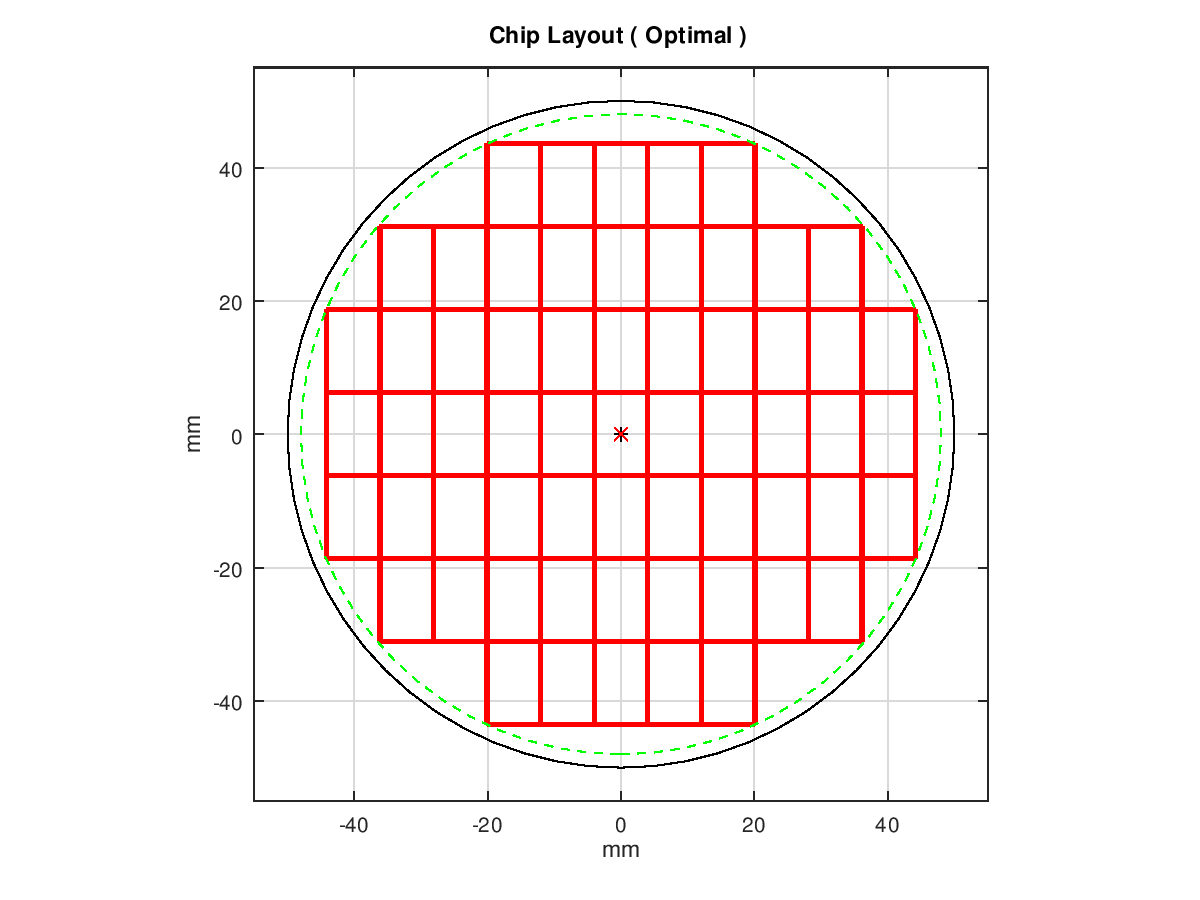
여기에서는이 형태로 레이아웃 설계 할 수 있다고합니다. 칩 면적이 100mm ² 에서 종횡비가 0.645로하면 가로 치수 8.035mm, 세로 치수 12.45mm 칩입니다. 다음 "배치 최적화"를 선택하고 필요한 항목을 입력하고 '계산 시작 "을 실행합니다. 나타난 페이지에 유효한 칩 수와 아래에 보이는 칩 레이아웃 그림이 표시됩니다. 마지막으로, 유효 칩 수가 기대했던 61 개임을 확인했습니다.

종횡비 최적화 계산 시간은 대충 유효 칩 수의 제곱에 비례합니다. 따라서 유효 칩 수가 50 개 미만이면 신경이 쓰이지 않습니다. 그러나 유효 칩 수가 50 개를 초과하면 계산 시간이 궁금 시작합니다. 100 개를 초과하면 계산을 중단하고 싶어집니다.
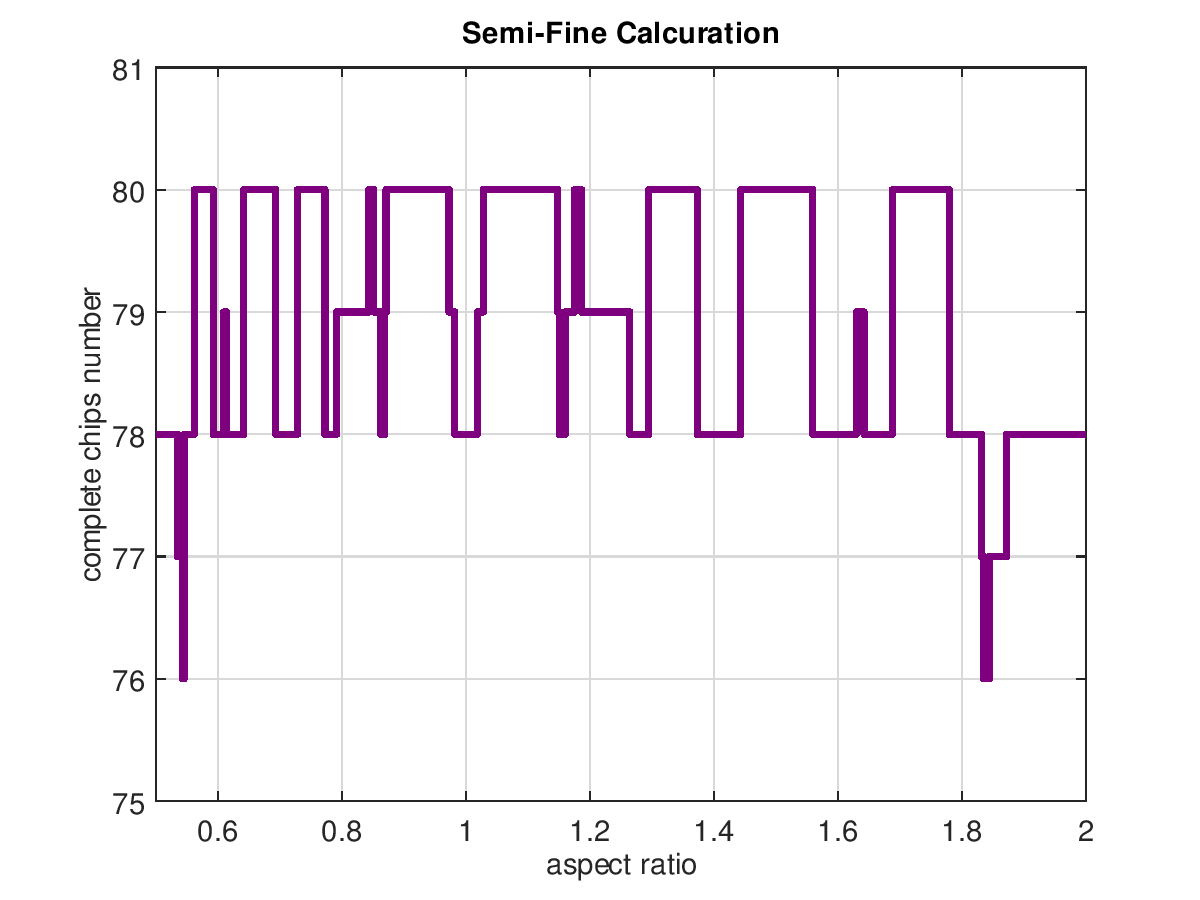
기다릴 수있는 인내의 한계는 사람 각자라고 생각 합니다만, 3 분이 한계라고 생각했습니다. 따라서 웨이퍼 직경 ² ÷ 칩 면적이 100 이상인 경우는 준 정밀 해법을 이용하기로했습니다. 이 해법은 웨이퍼 원형 중심이 칩 중심 또는 칩 격자 점을 통과하는 y 축과 평행 한 직선 상에있는 것을 후보 솔루션의 조건에 추가하여 열거 횟수를 줄입니다.
이 방법은 정밀 해법에 비해 계산 시간이 매우 짧습니다하지만 드물게 잘못된 결과를 제공합니다. 그러나 배열 최적화 계산에서 확인하면 큰 실수를 감수 걱정은 없습니다.
또한 정밀 해법으로 오해되지 않도록 그림의 선 색상을 파란색에서 보라색으로 바꾸고 제목도 Semi-Fine Calcuration 표시하고 있습니다. 오른쪽 그림은 칩 면적의 초기 값만을 75mm ² 에 한 것입니다.

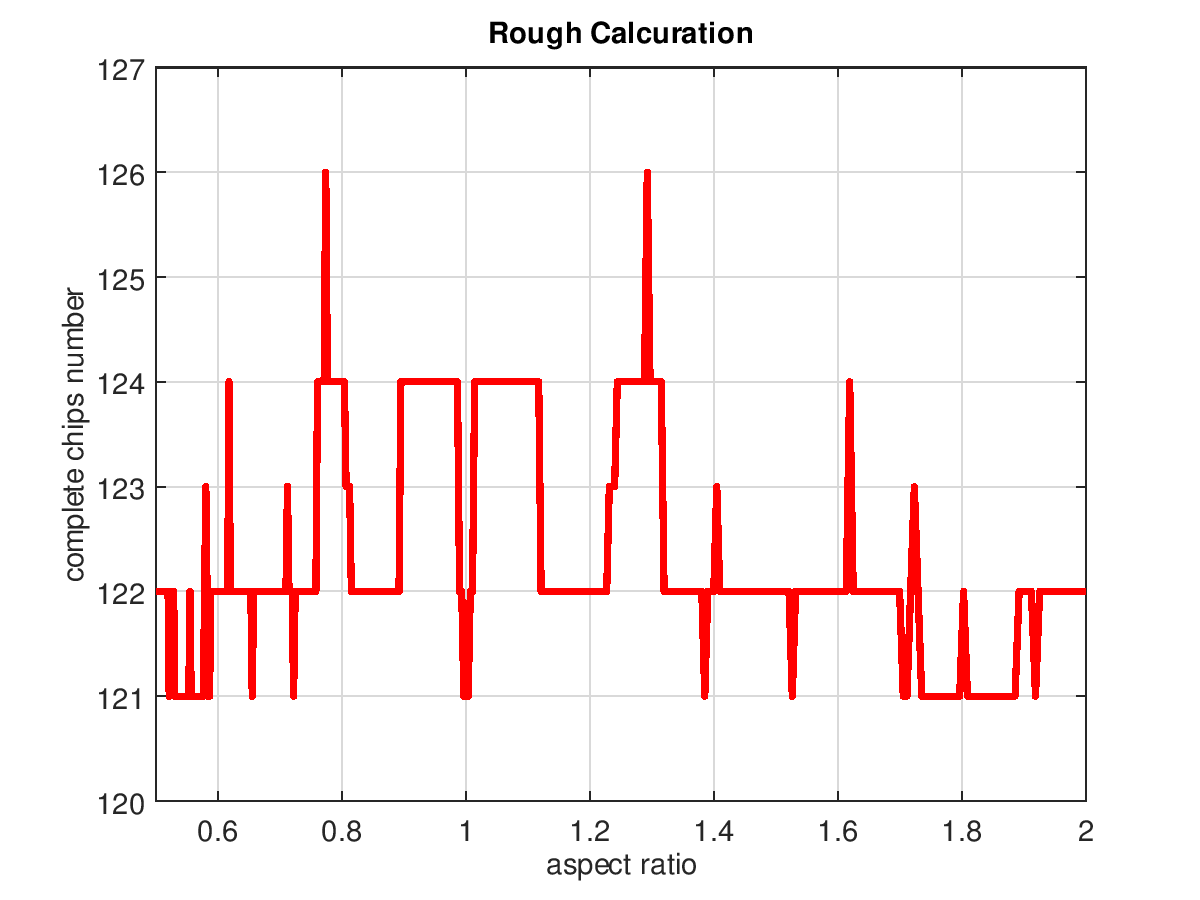
연합 정밀 해법에서도 유효 칩 수가 많을수록 계산 시간은 길어집니다. 따라서 웨이퍼 직경 ² ÷ 칩 면적이 150 이상인 경우는 준 정확한 해법은 적용하지 않습니다.
여기에서 적용한 알고리즘은 ① ~ ③합니다. ① 종횡비가 0.5에서 2.0의 범위에서 대수가 간격이되는 100 가지 종횡비를 정하는
② 이에 대해 배치 최적화를 적용한 경우의 최대 유효 칩 수를 공개 특허 (일본 특허 공개 2003-257843)의 방법으로 요구
③ 그 값을 꺾은 선 그래프로 연결

오른쪽 그림은 칩 면적의 초기 값만을 50mm ² 에 한 것입니다. 다른 해법과 구별 할 수 있도록 그래프의 색상을 빨간색 선으로 표시하고 있습니다.

그런데,이 경우에도 유효 칩 수가 최대 (126 개)가 될 종횡비의 범위는 좁아 잘 모르겠습니다. 또한, 계산이 정확 아니라 종횡비의 상하를 좁혀도 의미가 없다고 생각합니다.
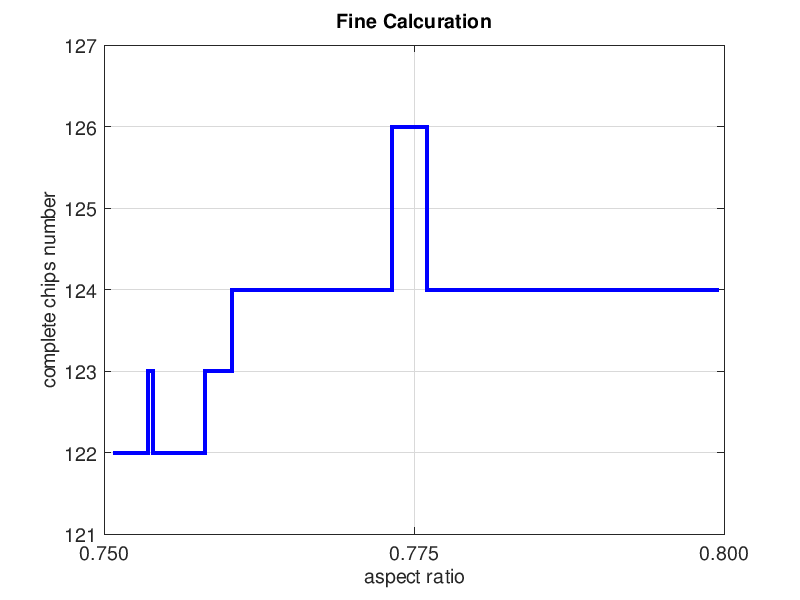
이러한 경우 종횡비 범위를 狭めれ하면 더 정확한 계산 방법을 선택할 수 있습니다. 실제 가로 세로 비율의 범위를 0.75 ~ 0.80로 변경하고 다시 계산하면 정확한 계산 방법을 선택합니다.