これから半導体のレイアウト設計を行う段階であれば「縦横比最適化」を選んでください．開いた入力画面で，6つの項目を設定します．
　①ウェーハ径
　②オリフラ長（零の場合はノッチタイプ）
　③インバリッドエリア
　④チップ面積
　⑤縦横比の最小値
　⑥縦横比の最大値
　①～⑥の初期値は自由に書き換えることが出来ますが，ここでの説明を理解して利用方法を学ぶため，最初は初期値のまま「計算開始」を実行します．
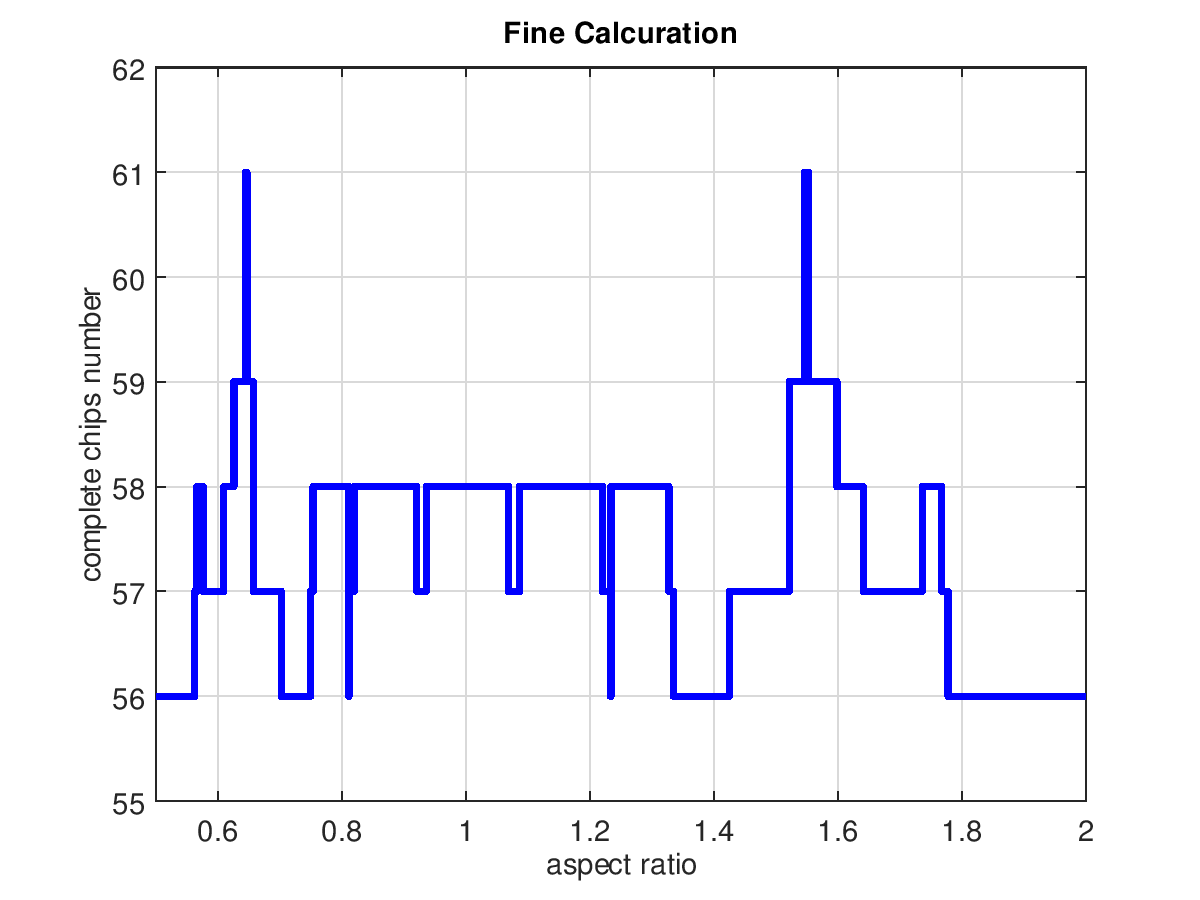
　30秒ほど待つと，横軸にチップ縦横比，縦軸に最大有効チップ数を示す右図が現れます．

これは，オリフラ長が零のときに起きる現象で，その理由は，縦横比が逆数のチップ形状は等しいからです．
　さて，有効チップ数が最大（61個）になる縦横比ですが，その範囲はとても狭くてよく分かりません．そこで，縦横比の上下限を少しずつ狭めては計算を繰り返すと，その縦横比が 0.65付近にあることが分かります．
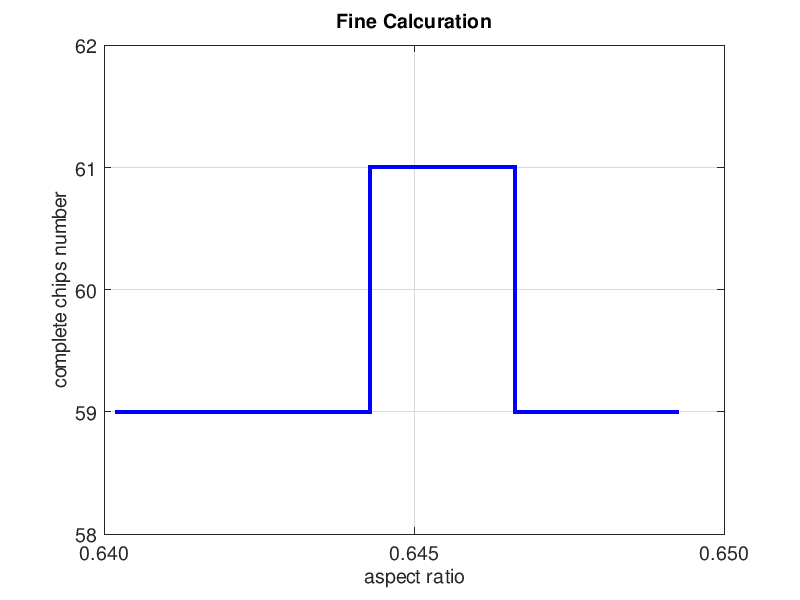
　右の図は，縦横比の範囲を 0.64～0.65 に変更して再計算した結果ですが，確かに，縦横比が0.645であれば有効チップ数は 61個になることが分かります．

　有効チップ数は，縦横比が 0.645付近で最大になりますから，その形状でレイアウト設計できるのであれば，それに越したことはありません．
　しかし，それが無理であれば，有効チップ数の多い別の縦横比を選びます．ただし，ここで終わりにしてはいけません．ごく稀にですが，計算誤差の影響で縦横比と有効チップ数の関係図に誤りがある場合があります．そのため，縦横比と有効チップ数の関係図を鵜呑みにせず，配置最適化を用いて有効チップ数の確認を行います．
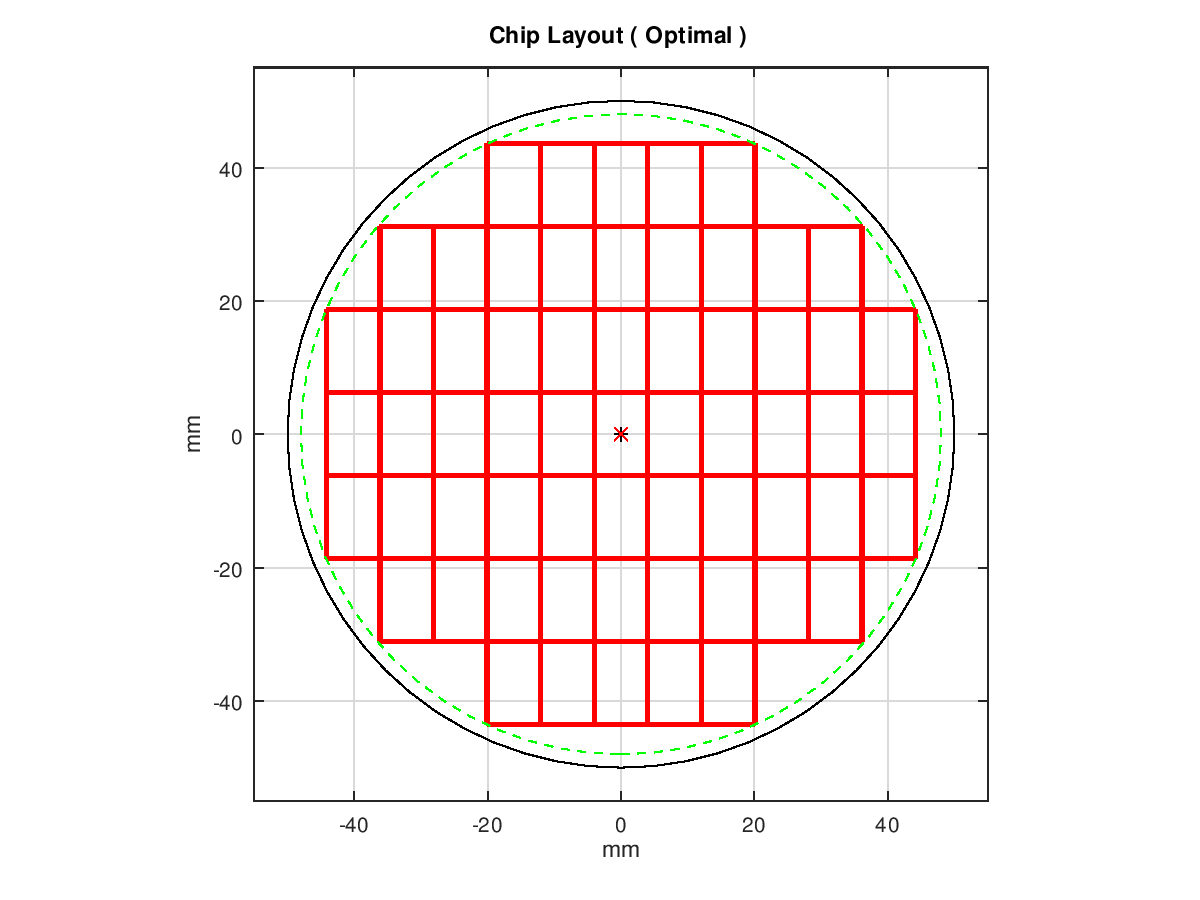
　ここでは，この形状でレイアウト設計できるとします．チップ面積が 100mm²で，縦横比が0.645とすれば，横寸法 8.035mm，縦寸法 12.45mmのチップになりますから「配置最適化」を選び，必要な項目に入力して「計算開始」を実行します．現れた画面には，有効チップ数と右に示すチップレイアウト図が表示されます．最後に，有効チップ数が期待していた61個であることを確認して完了です．

　縦横比最適化の計算時間は，凡そ有効チップ数の 2乗に比例しています．そのため，有効チップ数が 50個未満であれば気にもならないのですが，50個を超えると計算時間が気になり，100個を超えると，途中で止めたくなります．
　待つことのできる我慢の限界は，人それぞれだと思いますが，恐らく 3分が限界だと考えました．のため，ウェーハ直径²÷チップ面積が100以上の場合は，ウェーハ円中心の座標がチップ中心あるいはチップ格子点を通過する y軸と平行な直線上にあることを，有効チップ数が変化する候補解の条件に加え，数え上げる前の候補解を少なくする準精密解法を用いることにしました．
　この方法は，精密解法と比べて計算時間が非常に短いのですが，ごくまれに誤った結果を提示します．しかし，配列最適化の計算で確認すれば，大きなミスを冒す心配はありません．
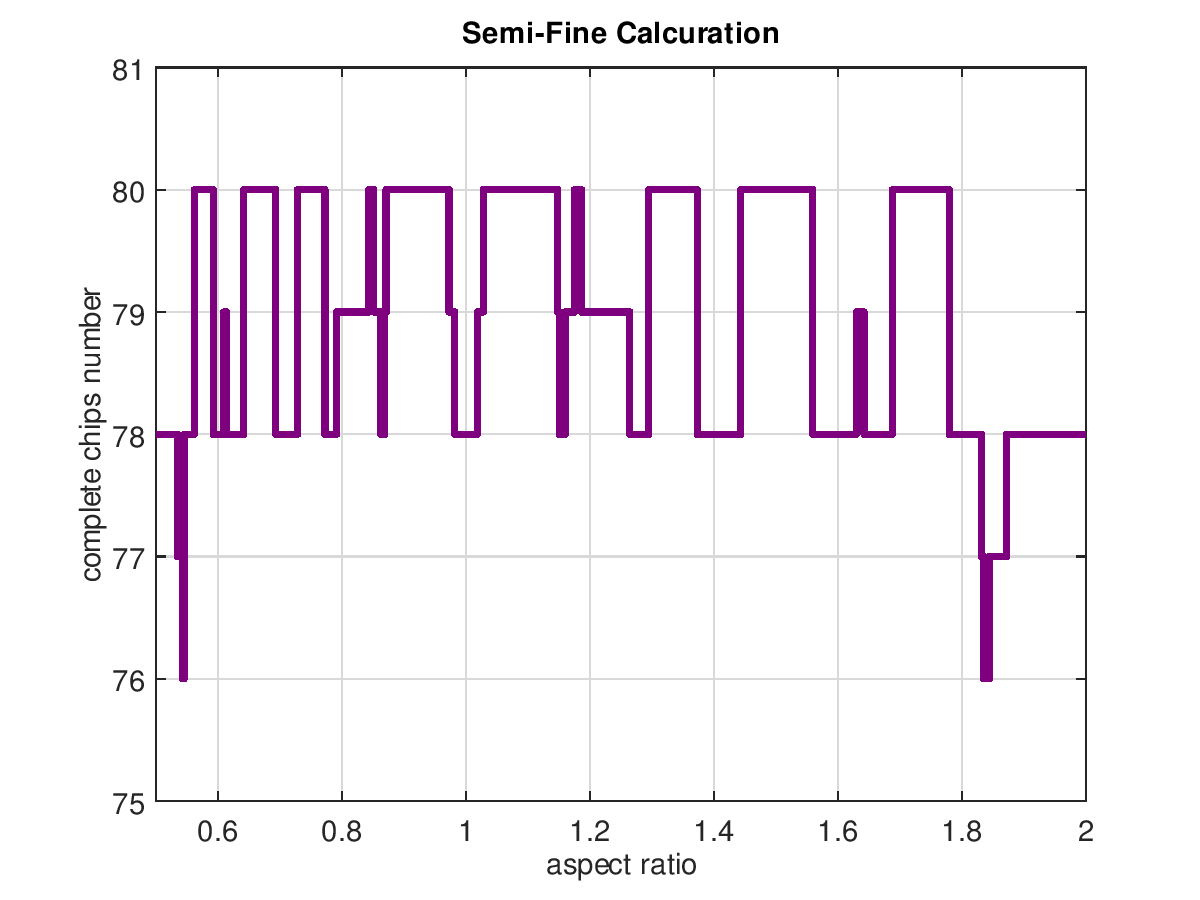
　なお，精密解法と誤解されないよう，図の折れ線の色を青から紫に変え，タイトルもSemi-Fine Calcurationと表示しています．右上の図は，チップ面積の初期値だけを75mm²にしたものです．

　準精密な解法でも，有効チップ数が多くなれば，計算時間は長くなります．従って， ウェーハ直径²÷チップ面積が150以上の場合は，準精密な解法は適用しないことにしました．
　ここで適用したのは，縦横比が 0.5 から 2.0の範囲で対数が等間隔となるように選んだ 100種類の縦横比に対して，配置最適化を適用した場合の最大有効チップ数を計算で求め，その値を折れ線グラフで結ぶという方法です．最大有効チップ数を公開特許（特開2003-257843）の方法で求めている点で，誰でも気付くことのできる単純な解法とは言えませんが，先の精密な解法よりは単純なので，素朴な解法と呼ぶことにしました．
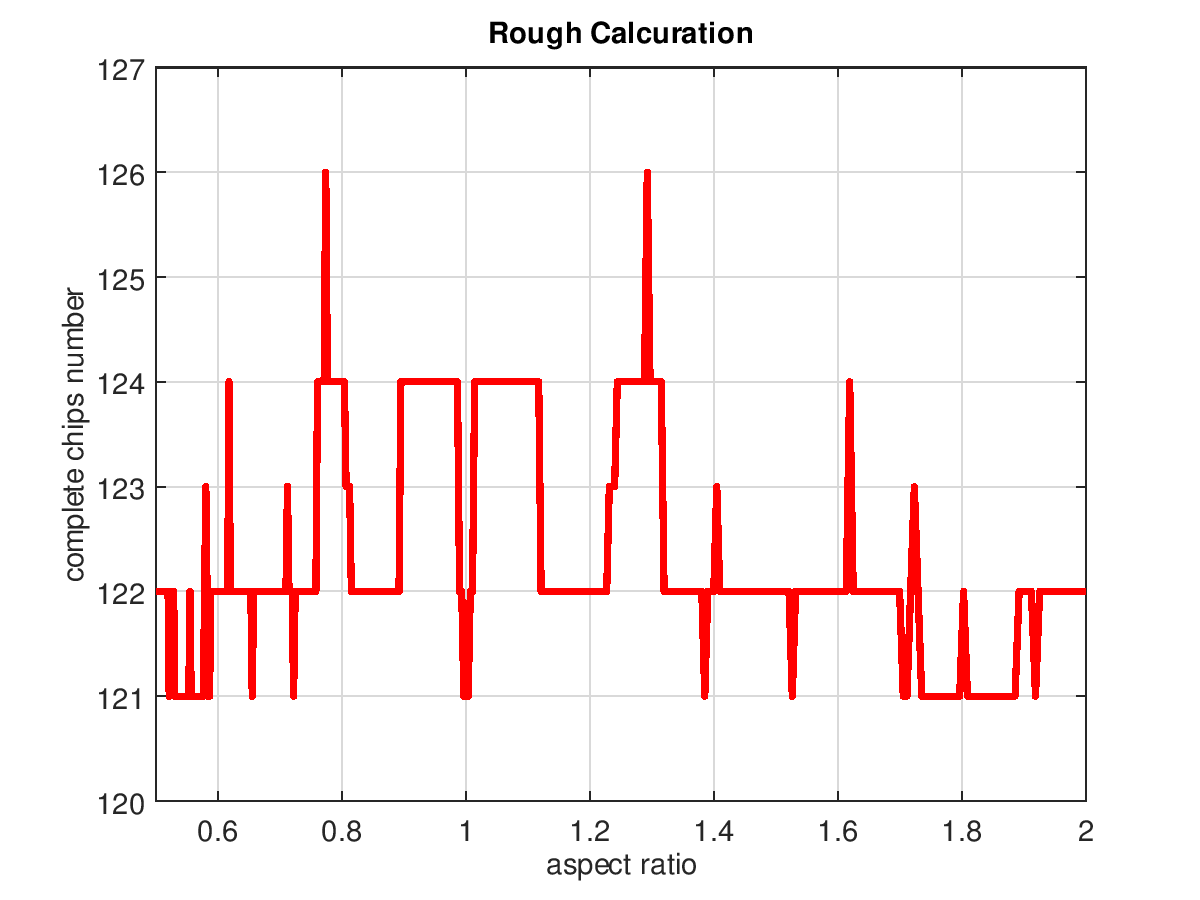
　右上の図は，チップ面積の初期値だけを50mm²にしたものです．他の解法と区別できるように，グラフの色を赤線で表示しています．

　さて，この場合も有効チップ数が最大（126個）になる縦横比の範囲は狭くてよく分かりません．おまけに，計算方法が精密でないため，縦横比の上下限を狭めても意味が無いように思われます．
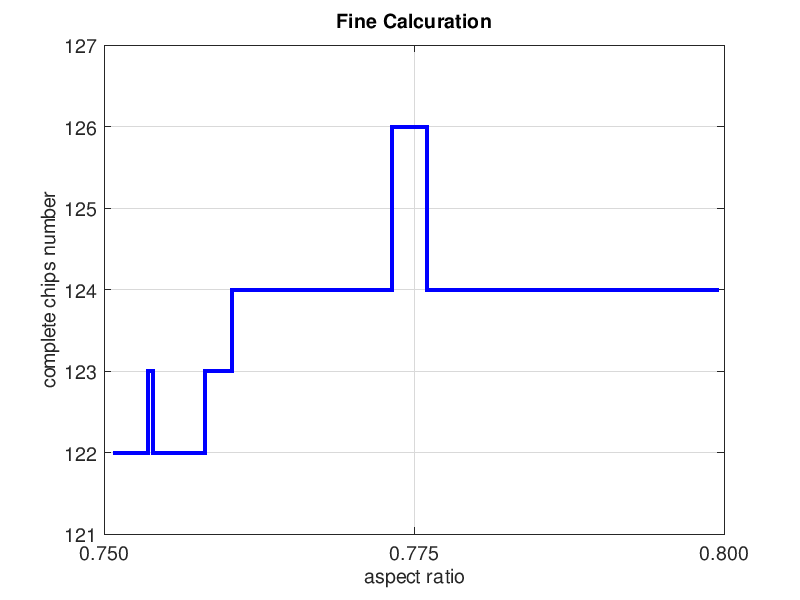
　しかし，有効チップ数が多い場合でも，縦横比の範囲を狭めれば，その狭さを考慮し，より精密な計算方法を選択するようにしています．実際，縦横比の範囲を 0.75～0.80 に変更して再計算すれば，精密な計算方法を選択します．