第8章 主成分分析
$\textbf{重回帰分析}$は,対象ベクトルを説明変数ベクトルの線形和で表した. 一方,$\textbf{主成分分析}$は,複数の対象ベクトルから逆に説明変数ベクトルを抽出する. 俗な言い方をすると,主成分分析は, 患者さんの病状(対象ベクトル)から可能性のある病名を割り出す$\textbf{診察}$に相当する. 一方,重回帰分析は,可能性の高い病名が分かっていて,どの病気に罹っているかを 確認する$\textbf{精密検査}$に相当する.簡単な例を使って説明する.本来は同じ波形が得られる実験を繰返し行って,$n$ 本の波形(ベクトル)を得たとしよう. このとき,何らかの原因で誤差が加わり,各波形は異なっていたとすると,解析者はこの未知なる原因を推察する必要がある. もし,原因と考えられる波形が同時に計測されていれば,重回帰分析をすればよいが, 結果の波形だけが多数存在するのみである.
このような場合,複数の波形 $\bf{X}=[\bf{x_{1},x_{2},...,x_{n}}]$ は,式(\ref{eqPrin_1})のように モデル化される.
\begin{equation} \bf{X}=\bf{Z\ a} \label{eqPrin_1} \end{equation} このとき,$\bf{Z}$ は,$X$ を構成する$n$ 本のベクトルから導いた互いに直交する $n$ 本の列ベクトルであり, $\bf{a}$ は $n \times n$ の正方行列である.
式(\ref{eqPrin_1})から,$Z$ を導くには固有値解析を用いる. 固有値解析の詳しいことを説明はしないが,ともかく,$Z$ は次の手順で求めることができる.
8.1 主成分ベクトルの算出手順
はじめに,式(\ref{eqPrin_2})から,実験波形の共分散行列 $\bf{S}$ を求める. \begin{equation} \bf{S}=\bf{X}^{\rm{T}}\ \bf{X} \label{eqPrin_2} \end{equation} 次に,共分散行列 $\bf{S}$ の固有値解析を行って,$n$ 本の固有ベクトルからなる行列 $\bf{V}$ と $n$ 個の固有値からなる対角行列 $\bf{D}$ を求める. scilabを用いれば,[ $\bf{V},\bf{D}$ ]=spec( $\bf{S}$ )で得られる. このとき,$\bf{S,V,D}$ には,式(\ref{eqPrin_3})の関係が成立している.\begin{equation} \bf{S\ V}=\bf{V\ D} \label{eqPrin_3} \end{equation} このとき,成分ベクトル群である $\bf{Z}$ は式(\ref{eqPrin_4})で表される. \begin{equation} \bf{Z}=\bf{X\ V} \label{eqPrin_4} \end{equation} なお,各固有値diag $(D)=[d_{1},d_{2},...,d_{n}]/\sum_{i=1}^{n}diag(D)$ は, $\bf{X}$ の総2乗和における各成分ベクトルの寄与率を示している.
つまり,固有値の大きい成分ほど重要である.
8.2 バーミラー計測の例
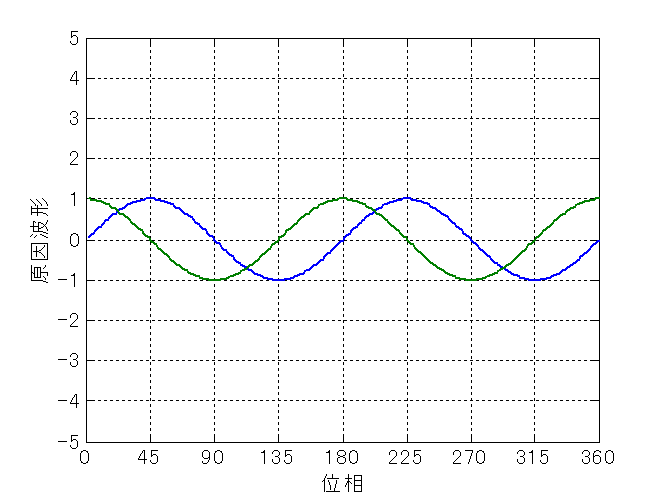
前節では,主成分分析の手順を述べた. ここでは,バーミラー形状計測を想定した例題を挙げ,主成分分析ができることを実際に示す. まず,図8.1の実線で示した波形がバーミラーの真の形状\mbox{ $y=9\sin(\pi x/180)$ }であったとする.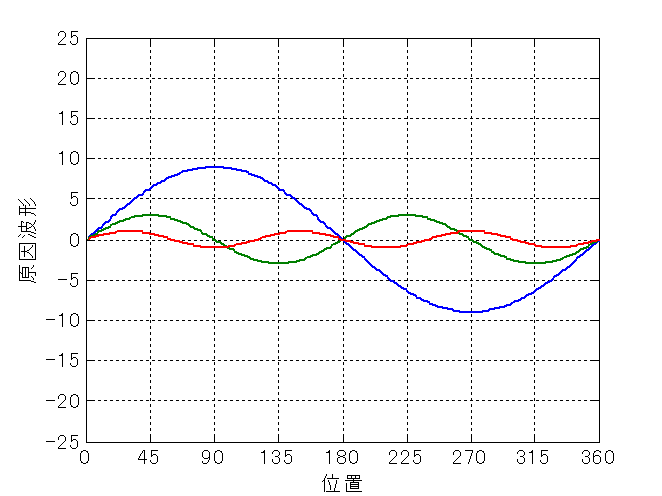
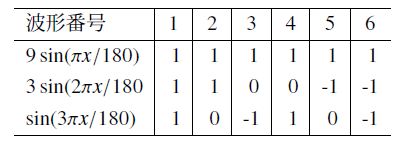
そして,何らかの物理的要因(例えば熱変形など)によって,破線で表した曲線 $y=3\sin(2\pi x/180)$ および一点鎖線で示した曲線 $y=\sin(3\pi x/180)$ の変形が現れたり現れなかったり, あるいは逆に現れたりしたとしよう.
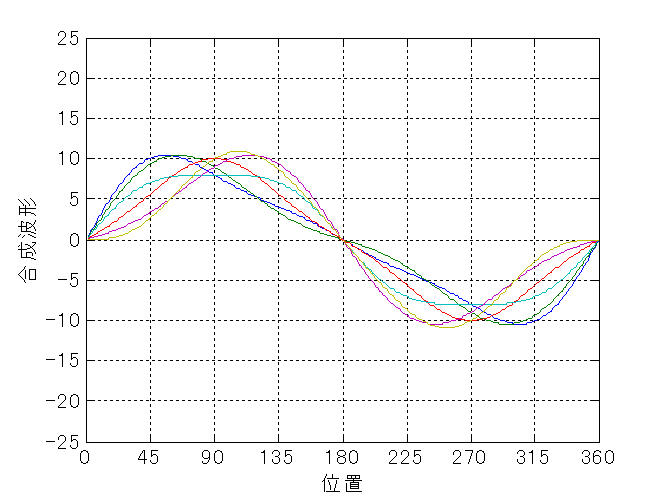
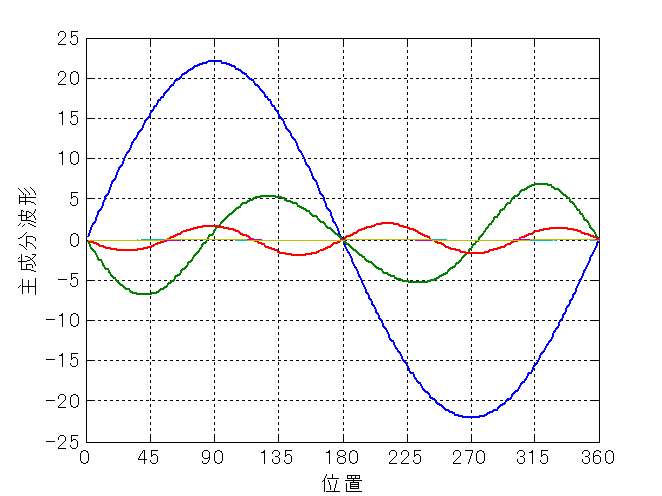
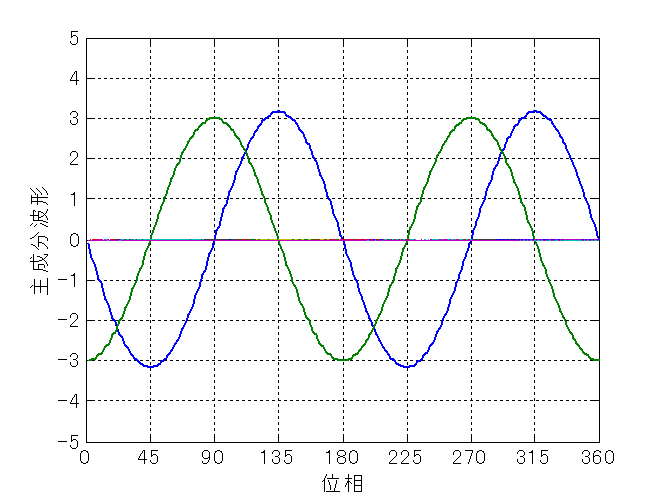
つまり,形状計測では,図8.2のように,6本の波形が得られたとする. このとき,主成分分析を行うと,計測して得られた図8.2の6本の波形から, 真の形状と何らかの物理的要因による変形形状を同時に導くことができる. 実際,この6本の波形を主成分分析すれば,図8.3の結果が得られる. 図8.1と比較すれば分かるように, バーミラー形状を支配する波形をかなり正確に示している.
8.3 位相の異なる一定周期波形の解析
周期的な波形を解析する場合,真っ先に思い浮かべるのはスペクトル解析だろう. しかし,スペクトル解析を適用するには,窓関数による両端処理が必要となる. 従って,スキャン中だけの断片的なデータにスペクトル解析を適用するとなれば, 中央部付近の形状しか分析できない. しかし,主成分分析を用いれば,窓関数処理を用いずとも分析できる. 多くの周波数成分が混入している場合は不向きだが,少数の周期波形が入り込んでいることを確認するには 大変便利な方法である. いま,図8.5に示すように,一定の周期で位相の異なる複数の波形が得られたとする. これらの波形について主成分分析を行うと,図8.6に示す2本の波形が得られる. この2本は位相が90度ずれた同じ周期の波形(正弦,余弦)である. つまり,周期は一定で位相が異なる波形は主成分分析で2本の波形に集約できる.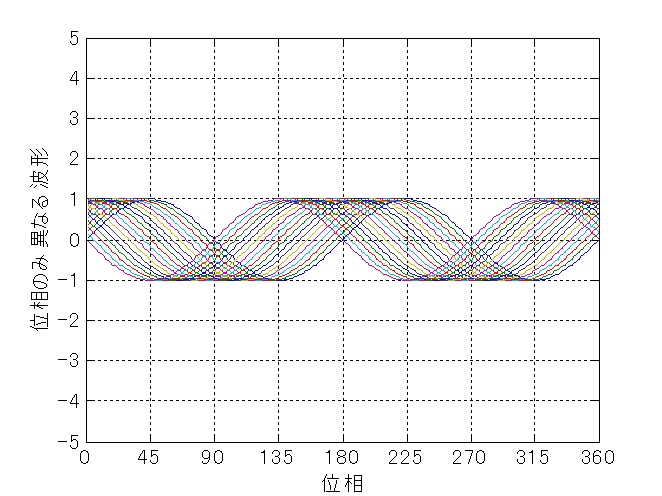
問題8.1
以下の表は,21人の身長,体重,胸囲,座高のデータである. これについて主成分分析を行い,固有値と固有ベクトルを示しなさい.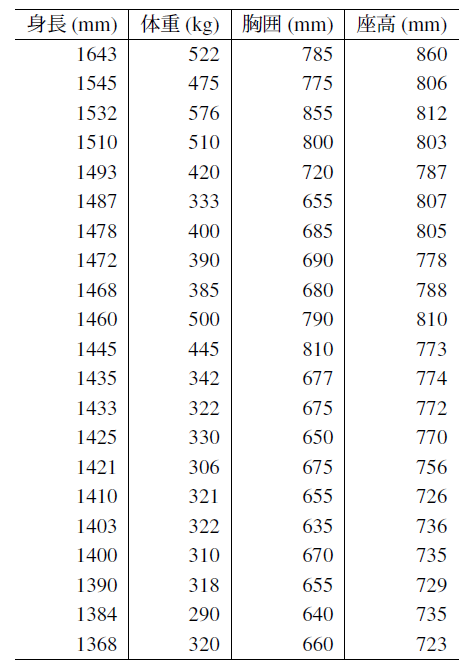
問題8.2
先の問題の固有行列において,各列が示す特徴をア~エの中から選びなさい.ア:胴長短脚度
イ:身体の太り具合
ウ:身体の大きさ
エ:下半身デブ度
