第4章 分散分析
回帰分析では,分析対象も説明変数も数量ベクトルであった. しかし,説明変数に相当する部分が非数量因子の場合もある. 例えば,体重に関係する非数量因子としては,性別,人種あるいは,おやつを食べる習慣の有無 などがある.恐らく無関係だろうが,血液型,星座なども挙げることができる.一般に「分散分析」とは,分散に占める非数量因子の成分を定量的に調べる方法である. 線形モデルから,分散を分析するのは「分散分析」ではないらしい. どうしてそんなことになったのか?未だに理解できない. ともかく,そういうものだと思うしかないのである.
さて,分散分析を用いる場合は2つに分けられる「データが与えられている場合」と 「これからデータを取る場合」である.後者は実験計画法に相当するので,後に回す. ところで,どの統計学の参考書も,分散分析は,分散分析表を作って,その結果からF検定するまで書いている. それはそれで構わないが,現実にF検定が必要となることは余りない. 分析表が出来れば十分である. どうして,「F検定は使わない」かと言うと, F検定は,分析する項目をどこまで選べばよいか?を決めるために使う. つまり,寄与率の低い項目まで分析するか?というどうでも良いことを検定している. 理屈では,実験数が極端に少なくて,寄与率の高い因子がF検定で棄却される場合も有りえるが, そんなケースは本当にあるのだろうか?ちょっと考え難い. 知っておいて損はないが,F検定はそれほど簡単ではないし,それより先に知っておいた方が良いことは山ほどある.
4.1 直交配置
データの2乗和や分散を分析するには,互いに直交する説明変数ベクトルを用いる. 数量ベクトルは,シュミットの直交化法で互いに直交なベクトルに変換できるが, 数量でない因子のベクトルは,シュミットの直交化法を使えない. この場合は,$\textbf{直交配置}$という方法を用いる. 各々の水準数が $m_{1}$ と $m_{2}$ の2つの因子において, 水準を示すベクトルを組合せたとき,$ m_{1} \times m_{2}$ 種類の全ての組み合わせが, 同じ回数だけ現れるとき,2つの因子ベクトルは互いに直交配置の関係にあると言う. この関係にあれば,因子Aの任意の水準のデータを選んだ時,因子Bの水準は均等に存在する. つまり,因子Bの影響は現れないから,直交配置なのである.4.2 n元配置
n元配置とは,分散分析の一元配置,二元配置として紹介される直交配置の総称である. n元配置のデータであれば,データ数は各因子の水準数の積に等しい. 例えば,ウエハ上の重ね合せマークでは,各データが,ウエハ番号,ショット番号,マーク番号などの属性を持っている. これらは数値で表されるが,順位数であって数量を示すものではない.つまり,非数量因子である. この場合因子は3つなので,三元配置となる. n元配置の分析項は $2^{n}$ 個ある.RAStoolの成分表は8列になっているが,これは三元配置であるからである.
いま,重ね合せ誤差の値を$x_{kji}$とする.ただし,$k=1,2,...,n$, $j=1,2,...,m$, $i=1,2,...,l$であり, $k$はウェーハの番号,$j$はショットの番号,$i$はマークの番号を示す. このとき,$x_{kji}$は次のように表すことができる. \begin{eqnarray} x_{kji} &=& \bar{ \bar{ \bar{x}}} \notag \\ &+&(\bar{ \bar{x}}_{k**}- \bar{ \bar{ \bar{x}}}) \notag \\ &+&(\bar{ \bar{x}}_{*j*}- \bar{ \bar{ \bar{x}}}) \notag \\ &+&(\bar{ \bar{x}}_{**i}- \bar{ \bar{ \bar{x}}}) \notag \\ &+&(\bar{x}_{kj*} - \bar{ \bar{x}}_{k**} - \bar{ \bar{x}}_{*j*} + \bar{ \bar{ \bar{x}}}) \notag \\ &+&(\bar{x}_{k*i} - \bar{ \bar{x}}_{k**} - \bar{ \bar{x}}_{**i} + \bar{ \bar{ \bar{x}}}) \notag \\ &+&(\bar{x}_{*ji} - \bar{ \bar{x}}_{*j*} - \bar{ \bar{x}}_{**i} + \bar{ \bar{ \bar{x}}}) \notag \\ &+&(x_{kji} - \bar{x}_{kj*} - \bar{x}_{*ji} - \bar{x}_{k*i} + \bar{ \bar{x}}_{k**} + \bar{ \bar{x}}_{*j*} + \bar{ \bar{x}}_{**i} - \bar{ \bar{ \bar{x}}}) \label{vari_eq2_7} \end{eqnarray}
右辺の8項は互いに直交しているので,その2乗和も8項に分解される. \begin{eqnarray} \sum_{k=1}^{K} \sum_{j=1}^{J} \sum_{i=1}^{I} x_{kji}^{2} &=& KJI\bar{ \bar{ \bar{x}}} ^{2} \notag \\ &+& JI \sum_{k=1}^{K} (\bar{ \bar{x}}_{k**}- \bar{ \bar{ \bar{x}}})^{2} \notag \\ &+& KI \sum_{j=1}^{J} (\bar{ \bar{x}}_{*j*}- \bar{ \bar{ \bar{x}}})^{2} \notag \\ &+& JK \sum_{i=1}^{I} (\bar{ \bar{x}}_{**i}- \bar{ \bar{ \bar{x}}})^{2} \notag \\ &+& I \sum_{k=1}^{K} \sum_{j=1}^{J} (\bar{x}_{kj*} - \bar{ \bar{x}}_{k**} - \bar{ \bar{x}}_{*j*} + \bar{ \bar{ \bar{x}}})^{2} \notag \\ &+& J \sum_{k=1}^{K} \sum_{i=1}^{I} (\bar{x}_{k*i} - \bar{ \bar{x}}_{k**} - \bar{ \bar{x}}_{**i} + \bar{ \bar{ \bar{x}}})^{2} \notag \\ &+& K \sum_{j=1}^{J} \sum_{i=1}^{I} (\bar{x}_{*ji} - \bar{ \bar{x}}_{*j*} - \bar{ \bar{x}}_{**i} + \bar{ \bar{ \bar{x}}})^{2} \notag \\ &+& \sum_{k=1}^{K} \sum_{j=1}^{J} \sum_{i=1}^{I} (x_{kji} - \bar{x}_{kj*} - \bar{x}_{*ji} - \bar{x}_{k*i} + \bar{ \bar{x}}_{k**} + \bar{ \bar{x}}_{*j*} + \bar{ \bar{x}}_{**i} - \bar{ \bar{ \bar{x}}})^{2} \label{vari_eq2_8} \end{eqnarray}
なお,RAStoolの分析表は,右辺の第4項と第5項を入れ替えて,[***], [k**], [*j*], [kj*], [**i], [k*i], [*ji], [kji]の順番に並べている. 式(\ref{vari_eq2_8})から,8項目に分散を分析する関数 sumsq3.m を次に示す.
function[S]=sumsq3(x,na,nb,nc)
%<機能>
%データの自乗平均を3つの属性によって
%オフセット成分と各変動成分および残差に分離
%<変数>
% x:データ
% na:第1属性のデータ数
% nb:第2属性のデータ数
% nc:第3属性のデータ数
% Soo:オフセット成分
% Sa:第1属性による変動成分
% Sb:第2属性による変動成分
% Sc:第3属性による変動成分
% Sab:第1属性と第2属性の交互作用による変動成分
% Sac:第1属性と第3属性の交互作用による変動成分
% Sbc:第2属性と第3属性の交互作用による変動成分
% Se:残差
C3=sum(x,1); % X...
Ca2=sum(reshape(x,nb*nc,na),1)'; % Xi..
Cb2=sum(reshape(x,nc,na*nb),1)';
Cb2=sum(reshape(Cb2,nb,na)',1)'; % X.j.
Cc2=sum(reshape(x,nc,na*nb)',1)'; % X..k
Cab1=sum(reshape(x,nc,na*nb),1)';
Cab1=reshape(Cab1,nb,na); % Xij.
Cac1=reshape(reshape(x,nc,na*nb)',nb,na*nc);
Cac1=sum(Cac1,1)';
Cac1=reshape(Cac1,na,nc)'; % Xi.k
Cbc1=sum(reshape(x,nb*nc,na)',1)';
Cbc1=reshape(Cbc1,nc,nb); % X.jk
N3=na*nb*nc;
Na2=nb*nc*ones(na,1);
Nb2=na*nc*ones(nb,1);
Nc2=na*nb*ones(nc,1);
Nab1=nc*ones(nb,na);
Nac1=nb*ones(nc,na);
Nbc1=na*ones(nc,nb);
M3=C3./N3;
Ma2=Ca2./Na2;
Mb2=Cb2./Nb2;
Mc2=Cc2./Nc2;
Mab1=Cab1./Nab1;
Mac1=Cac1./Nac1;
Mbc1=Cbc1./Nbc1;
Soo=M3*M3*N3;
Sa=sum(Na2.*(Ma2-M3*ones(na,1)).^2,1); % Sa
Sb=sum(Nb2.*(Mb2-M3*ones(nb,1)).^2,1); % Sb
Sc=sum(Nc2.*(Mc2-M3*ones(nc,1)).^2,1); % Sc
Sab=Mab1-ones(nb,1)*Ma2'-Mb2*ones(1,na)+M3*ones(nb,na);
Sab=sum(sum(Nab1.*Sab.^2)',1); % Sab
Sac=Mac1-ones(nc,1)*Ma2'-Mc2*ones(1,na)+M3*ones(nc,na);
Sac=sum(sum(Nac1.*Sac.^2,1)',1); % Sac
Sbc=Mbc1-ones(nc,1)*Mb2'-Mc2*ones(1,nb)+M3*ones(nc,nb);
Sbc=sum(sum(Nbc1.*Sbc.^2,1)',1); % Sbc
St=sum((x-M3*ones(nc*nb*na,1)).^2,1); % St
Se=St-(Sa+Sb+Sc+Sab+Sac+Sbc);
S=[Soo,Sa,Sb,Sc,Sab,Sac,Sbc,Se];
例として,二元配置のデータ$x_{ji}$を式(\ref{vari_eq2_9})のように分解し, その2乗和を式(\ref{vari_eq2_10})のように求めてみる.
まず,二元配置のデータ$x_{ji}$は次のように表すことができる.
\begin{eqnarray} x_{ji} &=& \bar{ \bar{x}} \notag \\ &+&(\bar{x}_{j*}- \bar{ \bar{x}}) \notag \\ &+&(\bar{x}_{*i}- \bar{ \bar{x}}) \notag \\ &+&( x_{ji} - \bar{x}_{j*} - \bar{x}_{*i} + \bar{ \bar{x}})\label{vari_eq2_9} \end{eqnarray} 右辺の4項は互いに直交しているので,その2乗和も4項に分解される.
\begin{eqnarray} \sum_{j=1}^{J} \sum_{i=1}^{I} x_{ji}^{2} &=& JI \bar{ \bar{x}} ^{2} \notag \\ &+& I \sum_{j=1}^{J} (\bar{x}_{j*}- \bar{ \bar{x}})^{2} \notag \\ &+& J \sum_{i=1}^{I} (\bar{x}_{*i}- \bar{ \bar{x}})^{2} \notag \\ &+& \sum_{j=1}^{J} \sum_{i=1}^{I} (x_{ji} - \bar{x}_{j*} - \bar{x}_{*i} + \bar{ \bar{x}})^{2} \label{vari_eq2_10} \end{eqnarray} 次に,第1因子の水準数を5,第2因子の水準数を4としたデータを乱数列で作り, その2乗和を4項目に分析してみる. ここでは,検証しやすいようにデータは整数とした.
表4.1の二元配置データについて,その2乗和を分析しよう.
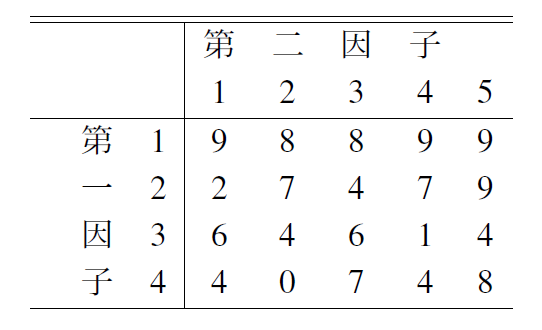
以下のプログラムを実行すると,表4.2の結果が得られる.
% Prog_Vari_1
clear;
close;
exec('sumsq2.sci'); % 二元配置の分散分析関数を宣言
x=[9 8 8 9 9; % データ入力
2 7 4 7 9;
6 4 6 1 4;
4 0 7 4 8];
x=matrix(x,20,1); % データを列ベクトルに並べ替え
S=sumsq2(x,5,4); % 分散分析
[S,sum(S)] % 分散分析結果の表示

問題4.1
三元配置の分散分析プログラム sumsq3.m と式(\ref{vari_eq2_10})を参考に, 二元配置の分散分析プログラム sumsq2.m を作成しなさい.問題4.2
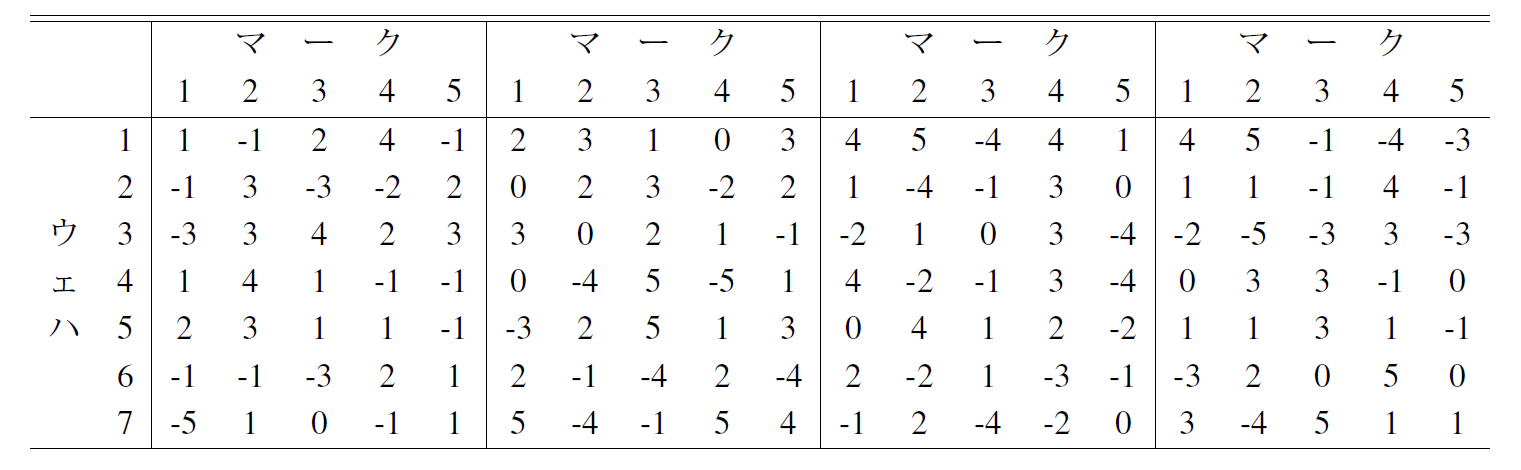
以下の表は,7ショット5点読みの二元配置データです. データの2乗和を分散分析しなさい.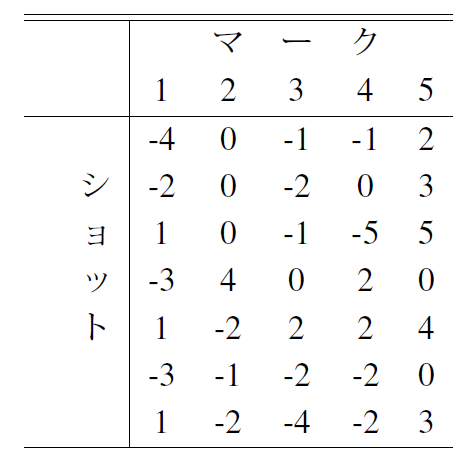
問題4.3
以下の表は,7ウェーハ4ショット5点読みの三元配置データです. データの2乗和を分散分析しなさい.