第9章 スペクトル解析
本章は,パワースペクトルによる周波数成分分析を説明する. また,信号収集時や解析上の注意事項として,サンプリング定理やトレンド除去,白色雑音の見分け方,短い波形データの扱い方を説明する.9.1 基本的な解析手順
一定の時間間隔 $dt$ で計測した信号ベクトル $\bf{y}$ が与えられていれば, matlabを用いてスペクトル解析ができる.matlabで次のように入力すると, 横軸に周波数,縦軸にパワースペクトルが表示される.>> [P,F]=pwelch(detrend(y))};
>> loglog(F/2/pi/dt,P)};
時間間隔 $dt$ の逆数をサンプリング周波数,その半分の周波数をナイキスト周波数 と呼ぶ.スペクトル解析の上限はナイキスト周波数である.ところで,パワースペクトルを周波数で積分すると重要な意味を持つ. 縦軸は分散となり,グラフは分散の周波数成分を示すからである. matlabで,次のように入力すれば表示できる.
>> semilogx(F*fs/2/pi,pi*cumsum(P)/length(F))}
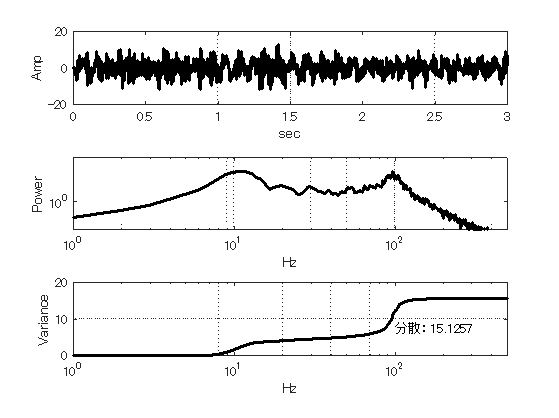
図9.1下段の図を見ると,この波の分散成分は10Hzで1/3,100Hzで2/3が分布していることが分かる. もし,このデータの分散を小さくするなら,100Hzの振動を抑制するのが効果的であり, 完全に抑制できるなら,分散を1/3にまで小さく出来ると予想がつく. このように,パワースペクトルを周波数で定積分すると,大変に役立つ.
参考に,パーセバルの公式を式(\ref{eq1128_0})に示す. この式は,波の振幅分散は周波数成分に分解できることを示している.
\begin{equation} \int_{-\infty}^{\infty} x^{2}(t)\ dt = \int_{-\infty}^{\infty} X^{2} (\omega)\ d\omega \label{eq1128_0} \end{equation} 図9.1 の解析ができるよう,matlab プログラム(Prog_Spec_1.m)を示しておく. ただし,描画の体裁に関連する部分は除いてある.
************************************************
% Prog_Spec_1.m
clear
close('all')
randn('state',1); % 乱数列固定
dt=0.001; % サンプリング周期
Fs=1/dt; % サンプリング周波数
T=3; % サンプリング時間
t=[0:dt:T]; % サンプリング時刻
zero=[-1 -5 0]*10*2*pi;
pole=[-1+i*10 -1-i*10 -10+i*100 -10-i*100 -30]*2*pi;
SYS=zpk(zero,pole,965);
G=tf(SYS); % 伝達関数の設定
x=1000*randn(size(t)); % 正規乱数
y=lsim(G,x,t); % 振動シミュレーション
[P,F]=pwelch(y); % スペクトル解析
subplot(311)
H=plot(t,y,'k');hold
set(H,'LineWidth',2);
set(gca,'Fontsize',10);
axis([0,3,-20,20]);grid
xlabel('sec');
ylabel('Amp')
subplot(312)
H=loglog(F*Fs/2/pi,P,'k');hold
set(H,'LineWidth',2);
set(gca,'Fontsize',10);
axis([1,500,1e-2,1e3]);grid
xlabel('Hz');
ylabel('Power')
subplot(313)
H=semilogx(F*Fs/2/pi,pi*cumsum(P)/length(F),'k');hold
axis([1,500,0,20]);
set(H,'LineWidth',2);
set(gca,'Fontsize',10);
ylabel('Variance')
xlabel('Hz');grid
H=text(100,7.5,['分散: ',num2str(std(y)^2)]);
set(H,'Fontsize',10);
************************************************
9.2 サンプリング定理
信号を計測するには,まず計測したい周波数領域を決める. 低域側の周波数が低いと計測時間が長くなり,高域側の周波数が高いとサンプリング周波数が高くなる.実際に計測するときは,カットオフ周波数がナイキスト周波数以下のローパスフィルタに通す. FFTアナライザを使用すれば,自動的にアナログフィルタをかけてくれる. しかし,自前のデータレコーダに記録する場合は注意が必要である. これを忘れると,データが台無しになる場合もある.
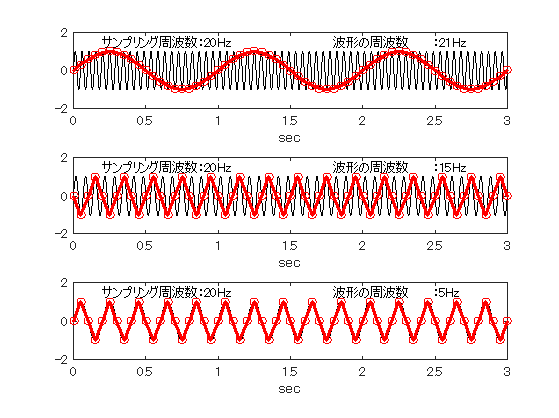
例えば,21Hzの正弦波をサンプリング周波数20Hzで計測すると, 図9.2上段に示した実線の21Hz波形は,破線で示す1Hz波形として計測されてしまう. このように,ナイキスト周波数より高い周波数成分は,ナイキスト周波数と0Hzで折り返された 周波数成分になる.これを折り返し誤差(エイリアシング)と呼ぶ. この場合,21Hzの波は10Hzと0Hzで折り返され,1Hzの波形に見えることがわかる.
一方,中段の図は,15Hzの正弦波をサンプリング周波数20Hzで計測した場合である. サンプリング周波数より低いがナイキスト周波数より高いため,やはり, 10Hzで折り返して5Hzの波形になる.
下段の図は,5Hzの正弦波をサンプリング周波数20Hzで計測した場合である. 10Hzのナイキスト周波数より低いので,正確に計測することができる.
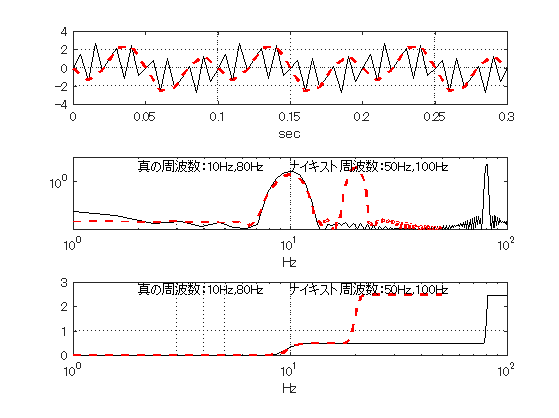
サンプリング定理に従わずにスペクトル解析した場合を考察する. 10Hzと80Hzの波形が合成した信号を,ナイキスト周波数100Hzで計測した場合(実線)と, 誤って50Hzで計測した場合(破線)を図9.3に示す. 上段の図は,取り込んだ信号を示しているが,実線と破線の波形は明らかに異なっている. 従って,中段に示したパワースペクトルも,本来80Hzにあるべきピークが50Hzのナイキスト周波数で 折り返し,20Hzになるのが分かる. なお,下段はスペクトルを周波数で積分した分散分布である.
9.3 トレンド除去と白色ノイズ
分散の計算をするとき,データから平均値を差し引くのと同じように, スペクトル解析でも,データから平均と傾き成分を除去する. 実際にトレンド成分を含んだデータを解析してみた.図9.4は,ドリフト成分を少し含んだデータ(実線)とドリフト成分を除いた データ(破線)をスペクトル解析した結果である. 低周波領域の値は異なるものの,10Hzと100Hzの周期波は分析されていて, 思ったほど問題はない.(もちろん,トレンド除去を忘れてはいけない)
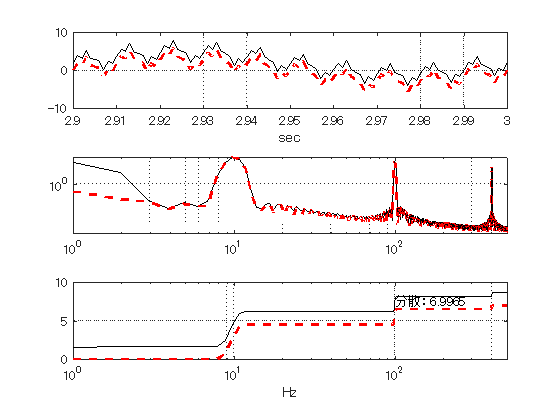
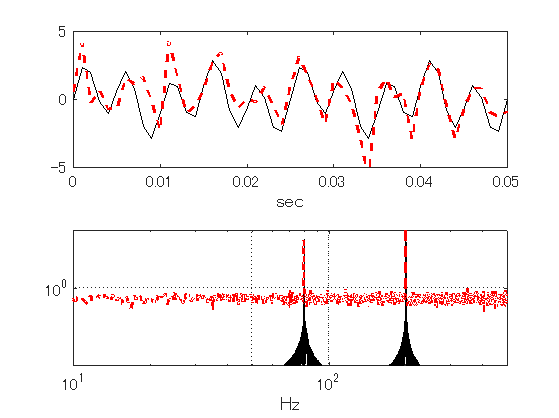
もう1つ,白色ノイズの問題がある. 単に主な周波数を発見するなら問題ないが,分散の周波数分析を行ったときに, 白色ノイズの影響を見誤まる可能性がある. 図9.5は,80Hzと200Hzである正弦波の合成波形とその波形にノイズを加えた2つの波形 とそれらのパワースペクトルを示す. 生の波形がそれほど異ならないのに,スペクトルには顕著な違いが現れ,全周波数領域の スペクトルが一様に増加している. これは,白色ノイズの持つ特徴である.
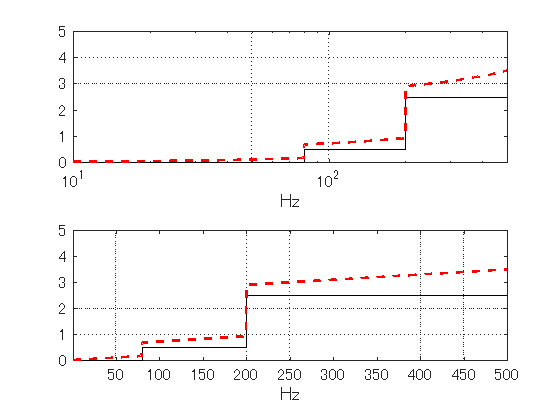
さて,このパワースペクトルを周波数で積分すると,図9.6の上図のようになる. 破線と実線の差は,白色ノイズの成分である. しかし,実際には白色ノイズを除いたスペクトルを表示することができない. 白色ノイズはフィルターを使っても取りきれないからである. 計測時間を長くすれば,スペクトルの精度は良くなるがノイズレベルはどうにも下がらない.
図示した例は,急峻なスペクトルなので見分けやすいが,そうでない場合は,周期スペクトルなのか? ノイズなのか分かりにくく,振幅を増加させている周波数を発見しにくい.
しかし,下図のように横軸を対数軸から標準に直すと,白色ノイズの成分は同じ傾きで 単調に増加する特徴があり容易に見分けることができる.
ここで,信号計測の注意事項をまとめておく
- 生信号を見て,アンプの状態,コネクタの接触,さらに定常性などを確認する
- ナイキスト周波数より低い周波数でローパスフィルタを入れて,信号計測する
- ドリフトで信号計測を失敗しないよう,バンドパスフィルタを入れる
9.4 データ長の短い波形
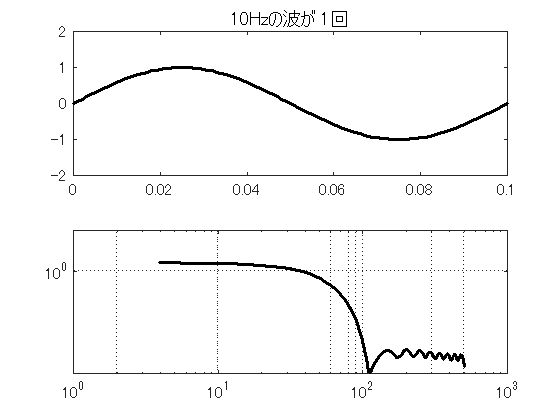
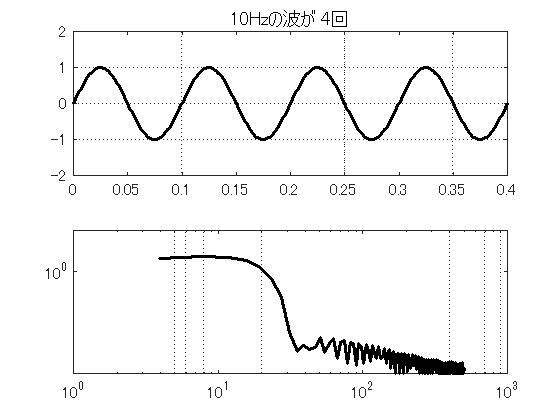
スペクトル解析は低周波領域の精度が低い. ところが,データ長の短いデータをスペクトル解析するケースが見受けられる. どうも,1波長分の波形でも解析できると思っているらしい. しかし,ある周波数成分を計測したいなら,最低でもその周期の10倍は計測したい. 精度良く計測するなら,20倍ぐらいは必要である.そこで,実際に1波長分しかない波形をスペクトル解析してみた. 図9.7~図9.10は,10Hzの波が1波長分だけのデータから20波長分まで, データ長を増加させながらスペクトル解析を行った結果である. 結果を見て分かるように,4周期以下しか含まないデータ長では,ピークも不明で全く計測できていない. 10周期でようやくピークらしきものが見え,20周期でピークは明瞭になる.
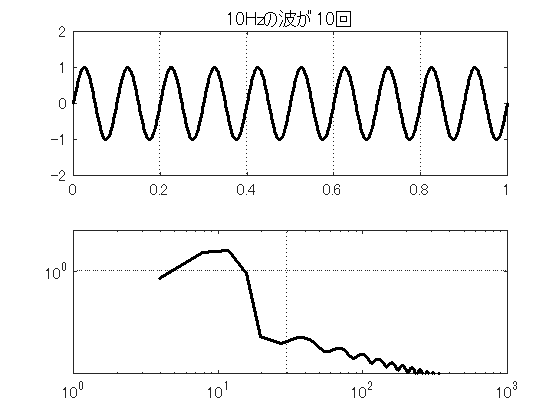
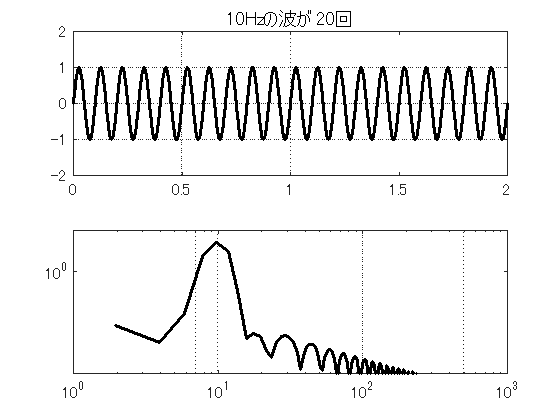
9.5 自己相関関数の利用
データ長の短い波形にスペクトル解析は適用できないが,周波数解析だけなら, 自己相関関数を求める方法で解析可能である. matlabでは,時間間隔 $dt$ の波形ベクトル $y$ を用意したら,次のように入力すればよい. 横軸にラグ時間,縦軸に相関係数のグラフが表示される.>> [C,lags]=xcorr(y,'coeff')};
>> plot(dt*lags,C)};
もし,波形が周期的であるなら,半周期ずらした波形との相関係数は負のピークを, 1周期ずらした波形なら正のピークになるので,波形に含まれる周期性を読み取ることができる. 図\ref{fig1128_B}は,1波長分の波形とその自己相関関数を示したものであるが, 自己相関関数が50msecで負のピークになっていることから,100msec周期つまり10Hzの周期性が あることを明示している.
図\ref{fig1128_C}は,3波長分の波形とその自己相関関数を示したものであるが, 自己相関関数の形状は変化しても100msecの周期性は問題なく読み取れる. このように,データ長が短くても自己相関関数を用いれば周波数の解析は可能である.
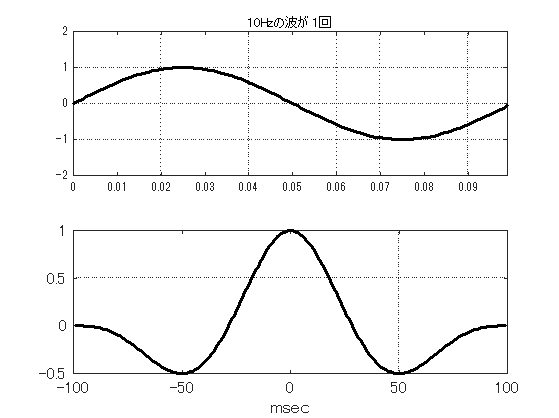
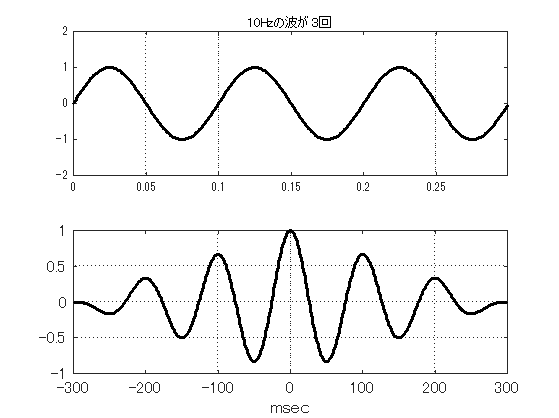
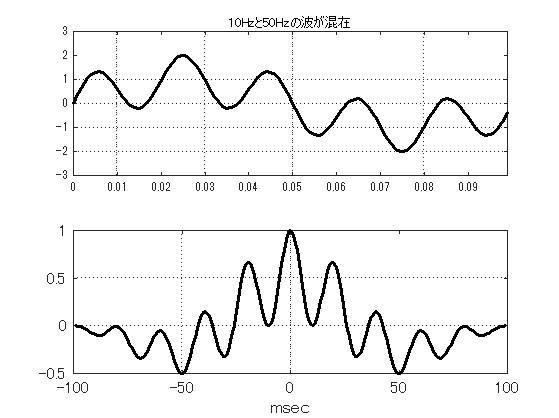
ところで,単純な波形は問題ないにしても,複数な合成波はどうだろう. 図\ref{fig1128_D}は,10Hzと50Hzの波形が合成されたものとその自己相関関数を示したものであるが, 負のピークからも半周期10msecと50msecの周期性,つまり50Hzと10Hzの成分がはっきり分かる.
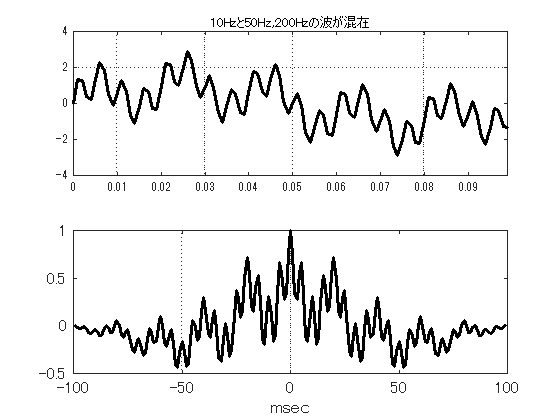
さらに200Hzの波形を合成したらどうだろう. 図\ref{fig1128_E}は,図\ref{fig1128_D}の波形に200Hzの波形を合成して, 10Hzと50Hz,200Hzの合成波形とその自己相関関数を示したものである. かなり読みづらくなったが,それでも3つの周期性を分析できる. ただ,これ以上に複雑化すると,相当に慣れた人でない限り解析は困難であろう.
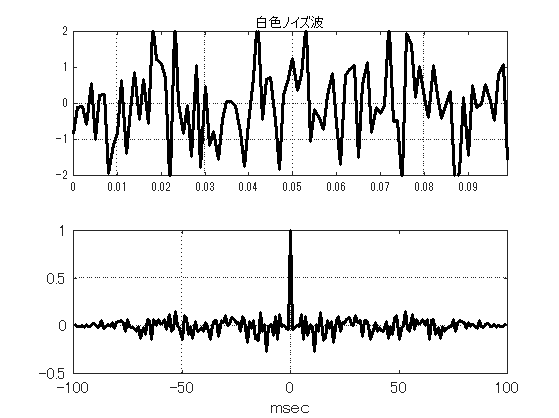
最後に,図\ref{fig1128_F}に白色ノイズとその自己相関関数を示してみた. ラグが0のとき以外の相関係数値は殆ど0となっていて,周期性のない波形の自己相関関数が どのようなものかお分かり頂けたと思う.
自己相関関数で周波数解析を行うには,ここで述べた知識が必要である. しかし,短い波形データを解析するときに発揮する威力は素晴らしいものがある. 是非活用されたい.
参考に,図9.11 と図9.12 の解析を行ったmatlabのプログラムを示しておく.
**************************************************************
% Prog_Spec_7.m
clear
close('all')
dt=0.001;
Fs=1/dt;
N=1000;
T=N*dt;
f=10;
t=[0:dt:dt*N];
% n周期分の正弦波を解析する
nf=Fs/f;
n=[1,3];
for ix=1:2
nf=n(ix)*Fs/f;
y=sin(2*pi*f*t(1:nf));
[C,lags]=xcorr(y,'coeff');
figure
subplot(211),H=plot(t(1:nf),y,'k');set(H,'LineWidth',2);
title(['10Hzの波が ',num2str(n(ix)),'回']);grid
axis([0,inf,-2,2]);
subplot(212),H=plot(1000*dt*lags,C,'k');set(H,'LineWidth',2);
set(gca,'FontSize',12);xlabel('msec');grid
end
**************************************************************
