第6章　ベイズ統計

　ベイズの定理で導かれる事後確率 $P(B_{i}|A)$ （ここでは $\pi_{2}(B_{i}|A)$ で表す） を使うのがベイズ統計学である． これは，事象 $A$ という客観的事実と事象 $B_{i}$ の主観的確率より導かれた確率であり， 現時点では，主観性と客観性の両方を扱える唯一の統計手法である． 一方，古典的統計学では実データしか扱えない． 実データ主義の強い統計的品質管理では，古典的統計学しか用いていないが， 近年は，品質の確率分布を予測する手段としてベイズ統計を利用するケースもでてきた． そこで，ベイズ統計学の考え方を解説する． なお，ベイズ統計学では尤度の概念が難しいので，そこに注意してほしい．

6.1　基礎知識

確率は，以下の3種類に分類できる．

• 理論的確率：サイコロの目など，理論的に求めることができる確率
• 客観的確率：実際のデータに基づいて計算される確率
• 主観的確率：経験や実績から設定される確率．例えば競馬のオッズ比など

このうち，主観的確率を利用できる方法が「ベイズ統計学」である． この方法の原理はベイズの定理によるが，その前に確率の乗法定理を理解しておく必要がある．

確率の乗法定理

$P(A \cap B_{i})$ ：事象 $A$ と事象 $B_{i}$ が同時に起こる確率（同時確率）
$P(A | B_{i})$ ：事象 $B_{i}$ の下で事象 $A$ が起こる確率（条件付き確率）
このとき，式(\ref{Bays_eq1})が成立する． \begin{equation} P(A \cap B_{i}) = P(B_{i} | A)P(A) = P(A | B_{i})P(B_{i}) \label{Bays_eq1} \end{equation}

ベイズの定理

$\sum_{i=1}^{n}P(B_{i})=1$ のとき，確率の乗法定理により式(\ref{Bays_eq2})が得られる． \begin{equation} P(B_{i}|A) = \frac{P(A|B_{i})P(B_{i})}{P(A)} = \frac{P(A|B_{i})P(B_{i})}{\sum_{i=1}^{n}P(A|B_{i})P(B_{i})} \label{Bays_eq2} \end{equation} ここで
$P(B_{i})$ ：事前確率．$\pi_{1}(B_{i})$ で表してもよい
$P(B_{i}|A)$ ：事象 $A$ が起きた条件下で事象 $B_{i}$ が起きる事後確率．$\pi_{2}(B_{i}|A)$ で表してもよい
$P(A|B_{i})$ ：事象 $B_{i}$ が起きた条件下で事象 $A$ が起きる確率．$f(A|B_{i})$ で表してもよい
　　　　：事象 $A$ が起きたときに事象 $B=B_{i}$ である尤度 $\ L(B_{i}|A)=f(A|B_{i})$ でもある．

6.2　確率分布予測例の紹介

簡単な2つの例題を用いて，ベイズ統計学の確率分布予測を説明する． 例1は事象が2つしかない離散的事象の問題である． 数式に積分が含まれないので分り易い． 一方，例2は事象が無限にある連続的事象の問題である． 現実の問題はこのタイプが多い．

例1：離散型事象の確率分布予測

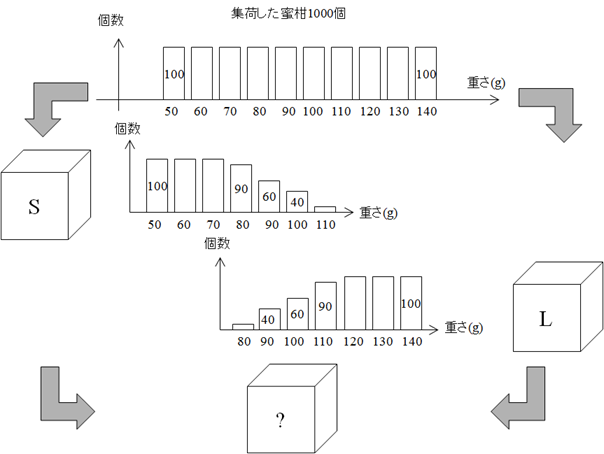
集荷場には1000個のみかんがあり， その重さは50g台～140g台まで100個ずつ分布していた． これらのみかんを大小に分別して2つの箱SとLに500個ずつ梱包した． このとき，SとLに入っているみかんの重さの分布は50g台～70g台のものはすべて箱Sに， 120g台～140g台のものはすべて箱Lに入っていたが，80g台～130g台は箱SとLの両方に分かれていた． その様子を表6.1と図6.1に示す．

表6.1　各箱に入っているみかんの個数(重量別)

みかんの重さ $x$ (g)	50	60	70	80	90	100	110	120	130	140
S	100	100	100	90	60	40	10	0	0	0
L	0	0	0	10	40	60	90	100	100	100

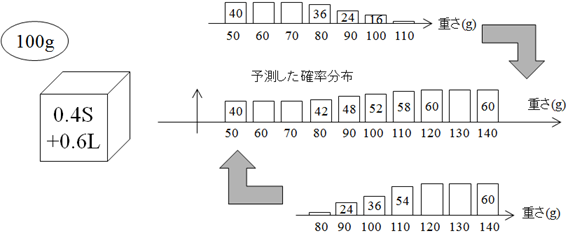
今，目の前にある箱の中にある蜜柑の重さ分布を予測したいのだが，箱がSかLか分らない． 何も情報が無い状態では，SあるいはLの箱を選択する事前確率 $\pi_{1}(S)$ と $\pi_{1}(L)$ は理論的に各々0.5である． ところで，各箱に入っている蜜柑の重さ $x$ の確率分布 $f(x|S)$ と $f(x|L)$ は 表6.1の値を個数で除したものになるから，表6.2になる． ここで，各箱に入っている蜜柑の重さの確率 $f(x|S)$ と $f(x|L)$ は，その箱がSまたはLである尤度でもある．

表6.2　各箱に入っているみかんの割合(重量別)

みかんの重さ $x$ (g)	50	60	70	80	90	100	110	120	130	140
x|S	0.20	0.20	0.20	0.18	0.12	0.08	0.02	0.00	0.00	0.00
x|L	0.00	0.00	0.00	0.02	0.08	0.12	0.18	0.20	0.20	0.20

よって，箱に入っている重さ $x$ のみかんの数 $n(x)$ は式(\ref{Bays_eq3})で予測される \begin{align} n(x) &= 500\times \{f(x|S)\pi_{1}(S)+f(x|L)\pi_{1}(L)\} \notag\\ &= 500\times \{f(x|S) \times 0.5+f(x|L) \times 0.5\} \label{Bays_eq3} \end{align} これを図6.2に示す．

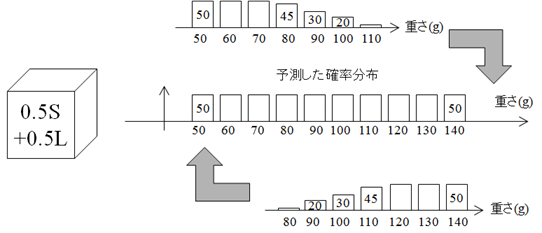
実際に計算すると，表6.3のように分布していると予想される． つまり，みかんを取り出す前は，どちらの箱の重さ分布も等しく考えていることになる．

表6.3　箱に入っているみかんの個数(事前予測)

みかんの重さ $x$ (g)	50	60	70	80	90	100	110	120	130	140
個数 $n(x)$	50	50	50	50	50	50	50	50	50	50

次に，箱から1つだけ取り出したみかんの重さが $w$ であったとすれば， 箱に入っている重さ $x$ のみかんの数 $n(x)$ は次式で予測される． \begin{equation} n(x) = 500\times \{f(x|S)\pi_{2}(S|w)+f(x|L)\pi_{2}(L|w)\} \label{Bays_eq4} \end{equation} このとき，事後確率 $\pi_{2}(S|w)$ と $\pi_{2}(L|w)$ は，ベイズの定理(式(\ref{Bays_eq2}))から得られる． \begin{equation} \pi_{2}(S|w) = \frac{f(w|S)\pi_{1}(S)}{f(w|S)\pi_{1}(S)+f(w|L)\pi_{1}(L)} \label{Bays_eq5} \end{equation} \begin{equation} \pi_{2}(L|w) = \frac{f(w|L)\pi_{1}(L)}{f(w|S)\pi_{1}(S)+f(w|L)\pi_{1}(L)} \label{Bays_eq6} \end{equation} いま，取り出したみかんが70gだったとき，各箱から70gの重さのみかんを取り出す確率(尤度)を考える． 70gのみかんは箱 $S$ にしか入っていないので，みかんを取り出した箱が $S$ であることは疑う余地がない． 一方，70gのみかんを取り出した箱が $S$ あるいは $L$ である事後確率 $\pi_{2}$ は 式(\ref{Bays_eq5}),(\ref{Bays_eq6})を用いて計算することができる． 実際，表6.3から，箱 $S$ と箱 $L$ の各々から70gのみかんを取り出す確率 $f(70g|S)$ と $f(70g|L)$ を求め， 式(\ref{Bays_eq5}),(\ref{Bays_eq6})に代入すれば，式(\ref{Bays_eq7}),(\ref{Bays_eq8})を得る． \begin{equation} \pi_{2}(S|70) = \frac{f(70|S)\pi_{1}(S)}{f(70|S)\pi_{1}(S)+f(70|L)\pi_{1}(L)} = \frac{0.2 \times 0.5}{0.2 \times 0.5 + 0 \times 0.5} = 1 \label{Bays_eq7} \end{equation} \begin{equation} \pi_{2}(L|70) = \frac{f(70|L)\pi_{1}(L)}{f(70|S)\pi_{1}(S)+f(70|L)\pi_{1}(L)} = \frac{0 \times 0.5}{0.2 \times 0.5 + 0 \times 0.5} = 0 \label{Bays_eq8} \end{equation} これは，至極当たり前の結果であるが， ベイズ統計の方法では，当たり前のことを当たり前の形で予測できていることが分かる． この場合，箱に入っている重さ $x$ のみかんの数 $n(x)$ は式(\ref{Bays_eq9})で予測される． \begin{align} n(x) &= 500\times \{f(x|S)\pi_{2}(S|70)+f(x|L)\pi_{2}(L|70)\} \notag\\ &= 500\times f(x|S) \label{Bays_eq9} \end{align} 式(\ref{Bays_eq9})から求められるみかんの重さの予測分布は，図6.3のようになる． このとき，$f(x|S)$ と $f(x|L)$ は各箱における蜜柑の重さの確率分布であると同時に，各箱の尤度でもある．

ところで，取り出したみかんが100gだったとする． このときも，各箱から100gの重さのみかんを取り出す尤度は表6.3から分かる． 箱$S$が0.08，箱$L$が0.12であるから，100gの重さのみかんを取り出した箱が$S$である確率は 0.4，$L$である確率は0.6となる． これは，箱$S$と箱$L$の各々から100gのみかんを取り出す確率と等しい． 表6.3から，尤度を式(\ref{Bays_eq5}),(\ref{Bays_eq6})に代入すれば， 式(\ref{Bays_eq10}),(\ref{Bays_eq11})を得る． \begin{equation} \pi_{2}(S|100) = \frac{f(100|S)\pi_{1}(S)}{f(100|S)\pi_{1}(S)+f(100|L)\pi_{1}(L)} = \frac{0.08 \times 0.5}{0.08 \times 0.5 + 0.12 \times 0.5} = 0.4 \label{Bays_eq10} \end{equation} \begin{equation} \pi_{2}(L|100) = \frac{f(100|L)\pi_{1}(L)}{f(100|S)\pi_{1}(S)+f(100|L)\pi_{1}(L)} = \frac{0.12 \times 0.5}{0.08 \times 0.5 + 0.12 \times 0.5} = 0.6 \label{Bays_eq11} \end{equation} よって，箱に入っている重さ$x$のみかんは式(\ref{Bays_eq12})で予測される． \begin{eqnarray} n(x) &= 500\times \{f(x|S)\pi_{2}(S|100)+f(x|L)\pi_{2}(L|100)\} \notag\\ &= 500\times \{f(x|S)\times 0.4+f(x|L)\times 0.6\} \label{Bays_eq12} \end{eqnarray} 式(\ref{Bays_eq12})から予測される分布は，表6.4，図6.4のようになる．

表6.4　箱に入っているみかんの個数($w=$100gを得た後の事後予測)

みかんの重さ$x$(g)	50	60	70	80	90	100	110	120	130	140
個数$n(x|100)$	40	40	40	42	48	52	58	60	60	60

{\bf 例2：連続的事象の確率分布予測}\\ ここでは，母数$\mu$と$\sigma$は不明だが，正規分布$f(t|\mu,\sigma)$であることが分っている性能$t$の確率分布を予測する． 実データは$n$個あるが，計測器は$w$以上の値を計測できないため， $r$個のデータは計量値があるが，「$n-r$個のデータは$w$以上」という曖昧なデータになっている． これらのデータを得た事象を$B$とする． ベイズ統計学の場合，はじめに$\mu$と$\sigma$の事前密度$\pi_{1}(\mu,\sigma)$を決めておかなくてはならない． $\mu$と$\sigma$は互いに独立であるとすれば式(\ref{Bays_eq13})となる． \begin{equation} \pi_{1}(\mu,\sigma)=\pi_{1}(\mu)\pi_{1}(\sigma) \label{Bays_eq13} \end{equation} $\mu$と$\sigma$の各事前密度は， 過去の実績を参考にして式(\ref{Bays_eq14})(\ref{Bays_eq15})のように 形状母数2のワイブル分布で設定した． なお，事前密度を正規分布に近づけたいなら形状母数を2.5にするとよい． \begin{eqnarray} \pi_{1}(\mu)&=&\frac{2(\mu-\mu_{0})}{h}\exp \Biggl(-\Bigl(\frac{\mu-\mu_{0}}{h}\Bigr)^{2}\Biggr) \label{Bays_eq14}\\ \pi_{1}(\sigma)&=&\frac{2(\sigma-\sigma_{0})}{g}\exp \Biggl(-\Bigl(\frac{\sigma-\sigma_{0}}{g}\Bigr)^{2}\Biggr) \label{Bays_eq15} \end{eqnarray} このとき，冒頭の事象$B$が起きた場合の事後密度$\pi_{2}(\mu,\sigma|B)$は式(\ref{Bays_eq16})で与えられる． \begin{equation} \pi_{2}(\mu,\sigma|B)=\frac{f(B|\mu,\sigma)\pi_{1}(\mu,\sigma)} {\int_{-\infty}^{\infty}\int_{0}^{\infty}f(B|\mu,\sigma)\pi_{1}(\mu,\sigma)d\sigma d\mu} \label{Bays_eq16} \end{equation} ここで， \begin{eqnarray} f(B|\mu,\sigma) \pi_{1}(\mu,\sigma) = {}_nC_r\Biggl(\int_{w}^{\infty} \frac{1}{\sqrt{2\pi}\sigma}\exp\Bigl(-\frac{(t-\mu)^{2}}{2\sigma^{2}}\Bigr)dt\Biggr)^{n-r} %\notag \\ %\times \prod_{i=1}^{r}\frac{1}{\sqrt{2\pi}\sigma} \exp\Bigl(-\frac{(t_{i}-\mu)^{2}}{2\sigma^{2}}\Bigr) \label{Bays_eq17} \end{eqnarray} 事後密度が分れば，性能$t$の確率分布$F(t|B_{i})$は式(\ref{Bays_eq18})で与えられる． \begin{equation} F(t|B) = \int_{0}^{\infty} \int_{0}^{\infty} f(t|\mu,\sigma) \pi_{2}(\mu,\sigma |B) d\mu d\sigma \label{Bays_eq18} \end{equation} 次に，式(\ref{Bays_eq13})～(\ref{Bays_eq18})を半導体露光装置の具体例にあてはめてみる． 図6.5}の黒＊印は，旧機種における露光装置数十台分のオーバーレイ精度データである． 今，新機種のオーバーレイ精度の確率分布を予測したいが， 新機種の実データは１つしかないとしよう． ただし，オーバーレイ精度の確率分布は平均$\mu$と標準偏差$\sigma$が未知でも，正規分布であることが経験的に確認されている． そこで，平均$\mu$と標準偏差$\sigma$は既存データの平均値$\mu_{0}=75.9$nmと 標準偏差$\sigma_{0}=1.52$nmを中心にワイブル分布していると仮定し， 各々の尺度母数は$h=75.9$nm，$g=1.52$nmであるとした．図6.6に平均$\mu$と標準偏差$\sigma$の 事前密度と事前分布を示す． 平均$\mu$と標準偏差$\sigma$の事前密度を与えれば，実データが得られる前の予測分布も決定する． 図6.7の細い点線は，事前密度だけで性能$t$の分布を予測したものである． 黒*印で示した前機種の性能分布と比較すると，その中央値はほぼ同じで，分布範囲は3倍程度広い． これは，事前の予測が前機種とほぼ同じ性能だが，データがない分だけ曖昧にしていることになる． いま， $t=7.5$nmという実データが1つ得られたとする． 式(\ref{Bays_eq16})で求めた事後密度と条件付の正規分布$f(t|\mu,\sigma)$を 式(\ref{Bays_eq18})に代入すれば，性能の確率予測分布は図6.7の太い実線で示したものになる．

問題6.1

　例1の問題では，S,L以外にもMという箱があり，そこには50g台～140g台までの蜜柑が50個ずつ入っていた． また，外見の記憶から目の前にある箱はMである可能性が高く，Mである可能性は50\%，S,Lは25\%と判断した． 一方，箱から取り出した蜜柑は90gであった．ベイズ統計学を用いて，箱がS,M,Lである確率を各々求めよ． また，箱の中の蜜柑の重さの分布を予測せよ．

問題6.2

　ベイズ統計学と古典的統計学の違いを一言で述べよ．