第7章 実験計画法
本章では,2水準だけのお手軽な実験計画法を紹介する.水準の制約はあるが簡単で実用的である.正規の実験計画法は直交表割り付けと分散分析,F検定が3点セットに なっている.しかし,F検定の必要性は少ない. また,分散分析は別の章で説明した. よって,ここでは直交表と割り付けを重点的に説明する.
実験計画法は,その名前から受ける印象から,笑い話のような誤解が多い. はじめに,実験計画法に関する注意事項を挙げておく.
(1) 実験計画法は,実験日程の立案手法ではない.
(2) 実験計画法は,要因実験(関係する要因を見究める実験)に用いる.
(3) 実験計画法は,各因子の分散成分を測るのが目的であり,そのモデルは決まっている.
(4) 実験計画法は,データの使い回し術である.
通常の実験は,検証や評価を目的とする実験が多い. これは,何かの知見を得るのが目的ではない.確認するだけである. 次に多いのは,実験式を作る実験である.アッベ係数の算出実験などが相当する. これは,既に実験式の構造が把握されている.
これらの実験は,「実験数が多くて実施できない」ということはないから, 実験計画法は必要ない. 実のところ,実験計画法を使うべき機会は余り多くない. (私は2回しか経験がない)
しかし,実験計画法は,現象の因果関係が不明である場合に効果がある. そのような場合,考えられる要因を変化させて影響の大きい要因を探る. こういう実験を要因実験という. このとき,枝分かれ図で実験条件を組み合わせると, 実験数は因子の水準数を累乗した数になる. 全て2水準でも5因子で $2^{5}=32$ 実験,7因子で $2^{7}=128$ 実験になる. 当然だが,因子数が増えれば実験数は急激に増加して実施不可能になる. そういう場合に実験計画法は役立つのである. どうして実験計画法だと少ない実験数で済むかと言うと, それは実験データを何回も使い回しているからである.
もしも実験計画法を知らないと,「仕方が無いから,関係ない因子は無視しましょう」と言って 勝手に因子を除外してしまう. 運悪く,その因子が重大な影響を持っていたら,その実験は無駄になる. だから,実験数を効率よく減らした一部実施要因実験つまり実験計画法は有効なのである.
ところで,要因実験は,なるべく多くの要因を少ない実験数で評価したい. だから,各因子の条件は2水準とするのが普通である. また,2水準の直交表は,アダマール行列なので容易に作れる. 多くの参考書では3水準の場合も説明しているが, 要因実験にわざわざ3水準の実験を行う必要はないと言える. よって,2水準以外の直交表は扱わない.
さて,要因実験における主効果と交互作用について説明する. 主効果は,各因子の分散成分である. 交互作用は,2つの因子の相乗・拮抗効果による分散成分を指す. しかし,現実に交互作用が大きくなることは稀だから,交互作用を考える必要はすくない. ただし,影響の大きい因子同士の交互作用は分析できるようにしておくべきだろう. そこで,主な因子間の交互作用と他の因子とが,なるべく同名関係 (交絡)にならないようにする.
余談だが,次に実験計画法を発展させたのは,品質工学やタクチメソッド で有名な田口玄一である.実験数を少なくする直交表の利用を提唱したが,日本では普及しなかった. そこで,米国に渡り,設計に応用するタグチメソッド(品質工学)を広めた. これについては,最後に触れる.
7.1 直交表と分散分析
直交配置の関係にある実験を行うには直交表を用いると便利である. ここでは,直交表と作り方と使い方を説明する.例えば,3つの因子A,B,Cの影響を受ける計測値 $y$ がある. 単純に考えて,3因子の2水準実験なら $2^{3}=8$ で8回の実験を行えば良い. 例えば,実験の数学モデルは式(\ref{Plan_eq1})~(\ref{Plan_eq8})のようになる. \begin{eqnarray} y_{1}=\bar{y}+p_{A}+p_{B}+p_{C}+\epsilon_{1}\label{Plan_eq1} \\ y_{2}=\bar{y}+p_{A}+p_{B}-p_{C}+\epsilon_{2}\label{Plan_eq2} \\ y_{3}=\bar{y}+p_{A}-p_{B}+p_{C}+\epsilon_{3}\label{Plan_eq3} \\ y_{4}=\bar{y}+p_{A}-p_{B}-p_{C}+\epsilon_{4}\label{Plan_eq4} \\ y_{5}=\bar{y}-p_{A}+p_{B}+p_{C}+\epsilon_{5}\label{Plan_eq5} \\ y_{6}=\bar{y}-p_{A}+p_{B}-p_{C}+\epsilon_{6}\label{Plan_eq6} \\ y_{7}=\bar{y}-p_{A}-p_{B}+p_{C}+\epsilon_{7}\label{Plan_eq7} \\ y_{8}=\bar{y}-p_{A}-p_{B}-p_{C}+\epsilon_{8}\label{Plan_eq8} \end{eqnarray} $y_{1}$~$y_{8}$ は計測値,$\bar{y}$ はその平均値,$+p_{A},+p_{B},+p_{C}$ が各因子の第一水準の影響, $-p_{A},-p_{B},-p_{C}$ が各因子の第二水準の影響,$\epsilon_{1}$~$\epsilon_{1}$ は誤差である. これを行列で表現すると式(\ref{Plan_eq9})になる. \begin{equation} \bf{y}= \left( \begin{array}{rrrr} 1 & 1 & 1 & 1\\ 1 & 1 & 1 &-1\\ 1 & 1 &-1 & 1\\ 1 & 1 &-1 &-1\\ 1 &-1 & 1 & 1\\ 1 &-1 & 1 &-1\\ 1 &-1 &-1 & 1\\ 1 &-1 &-1 &-1 \end{array} \right) \left( \begin{array}{c} \bar{y}\\ p_{A}\\ p_{B}\\ p_{C} \end{array} \right) +\bf{\epsilon} \label{Plan_eq9} \end{equation} このとき,要素が-1か1の値をとる8行4列の行列において,各列は互いに直交配置 (互いの条件が均等に組み合わされる)の関係にある.この係数行列を $\bf{K}$ とすると, $\bf{K}$ はアダマール(hadamard)行列から容易に抽出できる. アダマール行列とは,要素が-1か1の値をとる次数 $2^{n}$ の正方行列である. MATLABにはアダマール行列を生成するhadamardと言う組込関数が用意されているが, Scilabにはない. ただ,簡単なので自作すれば良い.
最も簡単なアダマール行列は, $\bf{H_{1}}=\left( \begin{array}{rr} 1 & 1 \\ 1 &-1 \end{array}\right) $ である.
次数 $2^{n}$ のアダマール行列を $\bf{H_{n}}$ であるとすれば,
次数 $2^{n+1}$ のアダマール行列 $\bf{H_{n+1}}$ は, $\left( \begin{array}{rr} \bf{H_{n}} & \bf{H_{n}} \\ \bf{H_{n}} &-\bf{H_{n}} \end{array}\right) $ となる.
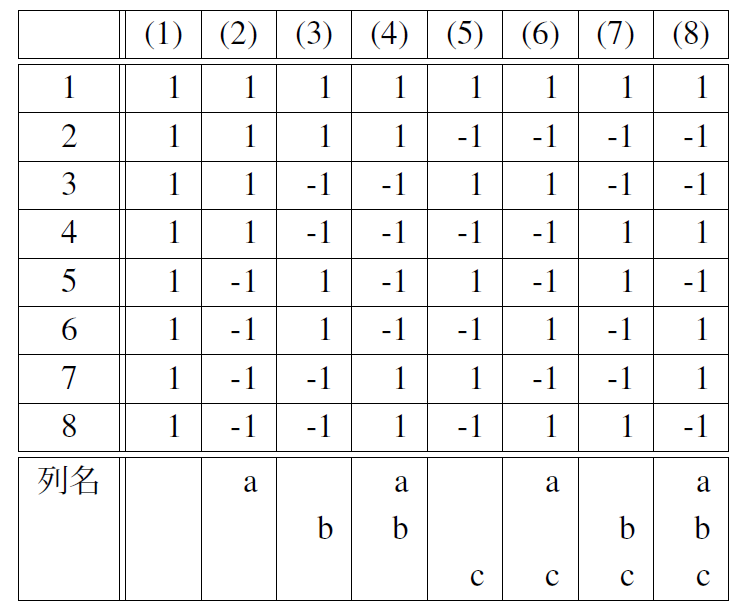
ところで,8次のアダマール行列で作った $L_{8}$ 直交表は表7.1になる. よく見ると,式(\ref{Plan_eq9})で用いられている係数行列は 直交表の1列,2列,3列,5列になっている. 1列目は平均値の成分を抽出するためのもので,通常の直交表には存在しない. 一方,2列目と3列目と5列目は列名があって各列の関係を示している. 例えば,列名がaとbの2列目と3列目を掛け合わせると4列目になる. つまり4列目は2列目と3列目の交互作用を示す. 今回,2列目と3列目と5列目を選んだのは互いの交互作用とだぶらないようにしたからである. もし,交互作用がだぶっても構わなければ,7つの因子まで分析可能である. つまり,3因子までしか分析できないと考えていた8実験は,実は7因子まで分析可能だったわけである.
さて,式(\ref{Plan_eq9})は式(\ref{Plan_eq10})で表される. \begin{equation} \bf{y}=\bf{Kp} +\bf{\epsilon} \label{Plan_eq10} \end{equation} 直交配置の関係を実現する $\bf{K}$ も実は直交行列であるので, 式(\ref{Plan_eq11})が成り立つ. また,$\bf{\epsilon}$ は,式(\ref{Plan_eq12})も成り立つ. なお,$I$ は単位行列である. \begin{eqnarray} \bf{K}^{\rm{T}}\bf{K}=n\bf{I} \label{Plan_eq11} \\ \bf{\epsilon}^{\rm{T}}\bf{K}=\bf{0} \label{Plan_eq12} \end{eqnarray} ここで,式(\ref{Plan_eq13})のようにして $\bf{y}$ の2乗和を求めると, $\bf{y}$ の分散成分は,回帰係数ベクトル $\bf{p}$ を求めれば良いことが分かる. \begin{eqnarray} \bf{y}^t\bf{y}&=&\bf{p}^{\rm{T}}\bf{K}^{\rm{T}}\bf{Kp} +2\bf{\epsilon}^{\rm{T}}\bf{Kp}+\bf{\epsilon}^{\rm{T}}\bf{\epsilon} \notag \\ &=&\bf{p}^{\rm{T}}\bf{p}+\bf{\epsilon}^{\rm{T}}\bf{\epsilon} \label{Plan_eq13} \end{eqnarray} 回帰係数ベクトル $\bf{p}$ を推定するには, 式(\ref{Plan_eq11})の両辺に左から $\bf{K}^{\rm{T}}$ を乗じればよい. これは,直交回帰分析に他ならない. \begin{equation} \bf{K}^{\rm{T}}\bf{y}=\bf{K}^{\rm{T}}\bf{Kp} +\bf{K}^{\rm{T}}\bf{\epsilon} \Rightarrow \bf{p} \label{Plan_eq14} \end{equation}
7.2 直交表の割り付け
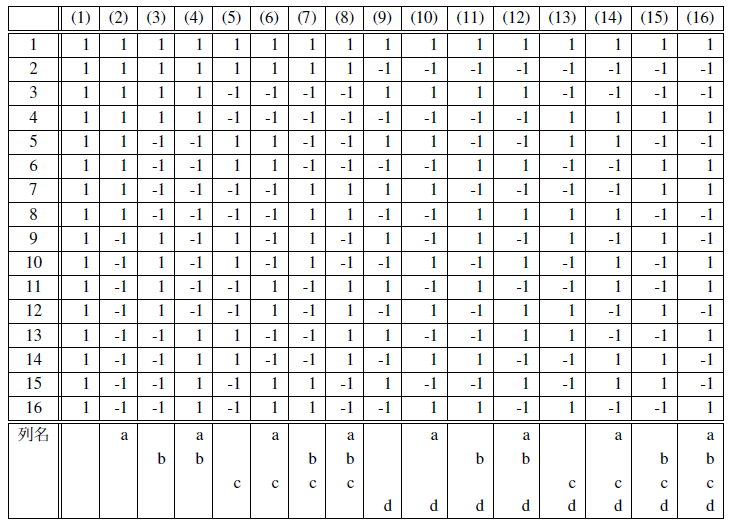
さて,各因子を行列 $\bf{K}$ の適当な列に割り付けよう.(ただし,第1列には割り付けない) ここでも,主要な因子間の交互作用が現れる列に,他の因子を割り付けないよう心がける. このとき,列名を使えば容易に交互作用が現れる列を探し出せる. 既に述べたように,列名がaと列名がbの交互作用は列名abの列になるが, 列名がabと列名がbcの交互作用は列名acの列になる. つまり列名に同じ記号があるとその記号は消去される.なお,要因実験は全体の様子を捉えるのが目的であるから, 水準の範囲は広く取る. 目的から逸脱しなければ,なるべく大胆な水準設定を心がける.
7.3 最も大切な実験の基本
ここでは,要因実験を含む実験全般について意見を述べる. 実験は思った以上に費用と時間がかかるものである. まず,以下のチェック事項に照らして,必要な実験であることを確認する.<実験する前のチェック事項>
・文献情報でも分ることを繰り返す実験でないか?(確認実験ではない)
・工場のデータでも読み取れる実験ではないか?
過去を振り返ると,目を覆いたくなる実験は多い. とりあえず,そういう実験をする人(させる人)の症状を挙げる.
<実験を失敗する人の症例>
(1) 実験計測値の数学モデルを意識しない.(結果だけが大事でメカニズムを考えない)
(2) 計測値に含まれる計測誤差を考えない.(計測誤差の範囲で,大小関係を議論している)
(3) 条件を振ろうとしない.(実演主義)
(4) 楽観的で高圧的(自分の仮説に酔う傾向があり,失敗しても反省しない)
たとえどんなに注意しても,1回だけの実験で終わらせることは難しい. しかし,言い訳できないお粗末な失敗は,ある程度防げる. その方法の1つは,予め実験の数学モデルを作り数値実験と解析をしておくことである. 特に,露光装置のように,限られた時間で実験する場合は,事前に結果も予測しておくことが大切である. それから,自分の予測と違う場合も想定しよう.周囲の人に相談して結果を予想をしてもらうのも良い. 最後に決めるのは自分だが,他人の考えは役に立つものである.
7.4 タグチメソッド(品質工学)
これは,品質の安定した製品設計と製造に寄与する. 決して高性能な製品ではない.使い方,使用環境,構成部品,組立公差など,色々な違いがあっても 期待した機能が保たれる製品を作ろうというのである. この価値観が理解できないと品質工学は理解できない. 品質工学では「一度でも合格したらOK」という製品は許されない.さて,機能の安定した製品はどうすれば作れるだろう? 簡単である.各々の誤差要因に影響されにくくすればよい.
第一は,誤差を小さくする.しかし,何でもかんでも小さくするのは無理だから, 影響の大きいものを厳しく管理し,そうでないものは放っておく.
第二は,誤差の影響を受けにくい設計パラメータを選ぶ.このような設計をロバスト設計という. タグチメソッドは,ロバスト設計をするための方法である. 誤差要因を変化させたときの性能変化をS/N比と定義し,S/N比の小さい設計を目指すのである.
ところで,誤差要因も設計パラメータも沢山あると,設計シミュレーションの試行回数も膨大になる. そこで,「直交表を使いましょう」ということになる. しかし,シミュレーションの試行回数は多く取れるから,無理に直交表を用いなくてよい. 相関係数の小さい乱数列を選んで近似的な直交行列を作れば,直交表の代わりになるので, それでも構わない. また,品質工学の唱える設計は,かなり以前より行われてきたように思う. 設計パラメータや誤差要因などの変動因子をランダムに変化させて, 最悪な条件でも機能を維持できる設計を探るのである. あるいは,影響度評価といって因子の回帰係数を比較評価していた. これは,品質工学ときわめて近い. つまり,品質工学は特別なものでも,新しいものでも,また,特に難しいものでもない.
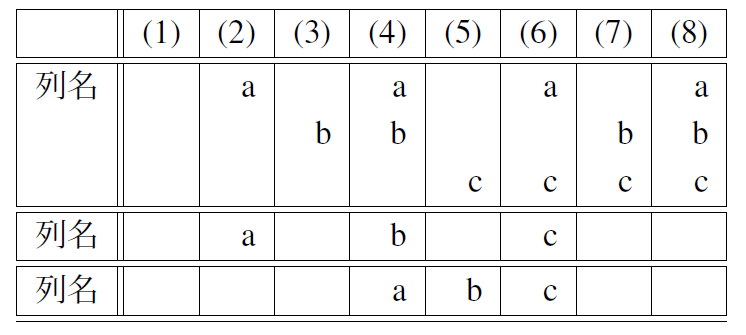
問題7.1
表7.1の第2列の列名をa,第4列の列名をb,第6列の列名をcとしたとき, 3列目から8列目で空いている列名を書きなさい. また,第4列の列名をa,第5列の列名をb,第6列の列名をcとしたとき, 3列目から8列目で空いている列名を書きなさい.