第3章 回帰分析
最も多用される数学モデルは線形モデルであり,これを推定するのが回帰分析である. カーブフィットも回帰分析であるから,利用経験のある人も多いだろう. しかし,1変数ずつの単回帰分析を行い,誤った結果を導いてしまう事例も多い. 最初から線形代数を用い,正しい回帰分析を身に付けるべきである.3.1 単回帰分析の公式を導く
回帰分析は最小2乗法そのものである.でも,線形代数に慣れていない人に, いきなり線形代数で最小2乗法を説明するのも酷であるから,説明変数が1つだけの単回帰から入る.単回帰式は式(\ref{Rgrs_eq1})で表される. \begin{equation} y_{i}=a_{0}+a_{1}x_{i}+e_{i}, \hspace{10mm}i=1,2,...,m \hspace{10mm} \\ \label{Rgrs_eq1} \end{equation} 回帰分析というのは,残差 $e_{i}$ の2乗和を最小にするよう,係数 $a_{0}$,$a_{1}$ を推定することである. 最初に,$e_{i}$ の2乗和を係数 $a_{0}$ と $a_{1}$ を含んだ式で表す. (ここが重要だが)もし,$a_{0}$ と $a_{1}$ が最適な値に推定されていたら, $e_{i}$ の2乗和を $a_{0}$ と $a_{1}$ で偏微分した値は零になる筈である. これを式(\ref{Rgrs_eq1_a}),(\ref{Rgrs_eq1_b})で表す. \begin{eqnarray} \frac{\partial}{\partial a_{0}} \sum_{i=1}^{m}e_{i}^{2} &=& \frac{\partial}{\partial a_{0}} \sum_{i=1}^{m}(y_{i}-a_{0}-a_{1}x_{i})^{2} \notag \\ &=& \frac{\partial}{\partial a_{0}} \sum_{i=1}^{m} (y_{i}^{2}+a_{0}^{2}+a_{1}^{2}x_{i}^{2}-2a_{0}y_{i}+2a_{0}a_{1}x_{i}-2a_{1}x_{i}y_{i}) \notag \\ &=& \sum_{i=1}^{m}(2a_{0}+2a_{1}x_{i}-2y_{i}) = 0 \label{Rgrs_eq1_a} \\ \frac{\partial}{\partial a_{1}} \sum_{i=1}^{m}e_{i}^{2} &=& \frac{\partial}{\partial a_{1}} \sum_{i=1}^{m}(y_{i}-a_{0}-a_{1}x_{i})^{2} \notag \\ &=& \frac{\partial}{\partial a_{1}} \sum_{i=1}^{m} (y_{i}^{2}+a_{0}^{2}+a_{1}^{2}x_{i}^{2}-2a_{0}y_{i}+2a_{0}a_{1}x_{i}-2a_{1}x_{i}y_{i}) \notag \\ &=& \sum_{i=1}^{m} (2a_{1}x_{i}^{2}+2a_{0}x_{i}-2x_{i}y_{i}) = 0 \label{Rgrs_eq1_b} \end{eqnarray} これより,$a_{0}$ と $a_{1}$ は式(\ref{Rgrs_eq1_c}),(\ref{Rgrs_eq1_d})で求められる. \begin{eqnarray} a_{0}&=&\frac{\displaystyle \sum_{i=1}^{m} x_{i}y_{i}\sum_{i=1}^{m} x_{i}-\sum_{i=1}^{m} x_{i}^{2}\sum_{i=1}^{m} y_{i}} {\displaystyle (\sum_{i=1}^{m} x_{i})^{2} -m\sum_{i=1}^{m} x_{i}^{2}}\label{Rgrs_eq1_c} \\ \notag\\ a_{1}&=&\frac{\displaystyle \sum_{i=1}^{m} x_{i} \sum_{i=1}^{m} y_{i}-m\sum_{i=1}^{m} x_{i}y_{i}} { \displaystyle (\sum_{i=1}^{m} x_{i})^{2} -m\sum_{i=1}^{m} x_{i}^{2}}\label{Rgrs_eq1_d} \end{eqnarray}
3.2 回帰分析の公式を導く
さて,式(\ref{Rgrs_eq1})を線形代数で表すと,式(\ref{Rgrs_eq2})で書き換えることができる. \begin{equation} \bf{y}=\bf{Xa}+\bf{e}, \hspace{10mm}\bf{y},\bf{e} \in {\bf R^{m}}, \ \ \bf{X} \in \bf{R}^{m \times n}, \ \ \bf{a} \in \bf{R}^{n} \hspace{10mm} \\ \label{Rgrs_eq2} \end{equation} ただし,$\bf{X}^{\rm{T}}\bf{X}$ は正則であるとする.ここでも,未知な係数ベクトル $\bf{a}$ を導く. 先ず,式(\ref{Rgrs_eq2})の $\bf{a}$ が $\bf{e}$ の2乗和を最小化する解ベクトルであるとする. このとき,$\bf{e}$ に $\bf{X}$ の成分は含まれていないから,式(\ref{Rgrs_eq2_a})が成立する. \begin{equation} \bf{X}^{\rm{T}}\bf{Xa}= \bf{X}^{\rm{T}}\bf{y} \label{Rgrs_eq2_a} \end{equation} 両辺の左側から逆行列 $(\bf{X}^{\rm{T}}\bf{X})^{-1}$ を乗じれば,式(\ref{Rgrs_eq2_b})で最小2乗解 $\bf a$ が得られる. \begin{equation} \bf{a}= (\bf{X}^{\rm{T}}\bf{X})^{-1} \bf{X}^{\rm{T}}\bf{y} \label{Rgrs_eq2_b} \end{equation}
$\textbf{追記1}$
式(\ref{Rgrs_eq2_a})が分らないという意見があったので, 「 内積 $\bf{e}^{\rm{T}}\bf{e}$ が最小であれば,$\bf{e}^{\rm{T}} \bf{X} = (0,0,...,0)$である 」を証明するため, 対偶命題を証明する.
$\textbf{証明はじめ}$
$\textbf{対偶命題:}$
「式(\ref{Rgrs_eq2})において,$\bf{e}^{\rm{T}}\bf{X}\neq (0,0,...,0)$ であれば,$\bf{e}$ の2乗和である内積 $\bf{e}^{\rm{T}}\bf{e}$ は,最小でない」
まず,$\bf{f}^{\rm{T}}\bf{X}= (0,0,...,0)$ である $\bf{f}$ を定義すると,$\bf{e}$ は次式で表される.
$\hspace{10mm}$ $\bf{e}=\bf{Xb}+\bf{f}$}
このとき,次式から,$\bf{e}^{\rm{T}}\bf{e}$ が最小でないのは明らかである.
$\hspace{10mm}$ $\bf{e}^{\rm{T}}\bf{e} = \bf{(Xb)}^{\rm{T}}\bf{Xb}+\bf{f}^{\rm{T}}\bf{f} \geq \bf{f}^{\rm{T}}\bf{f}$
よって,$\bf{e}^{\rm{T}}\bf{e}$ が最小であれば,$\bf{e}^{\rm{T}} \bf{X} = (0,0,...,0)$ であると言える.
$\textbf{証明おわり}$
$\textbf{追記2}$
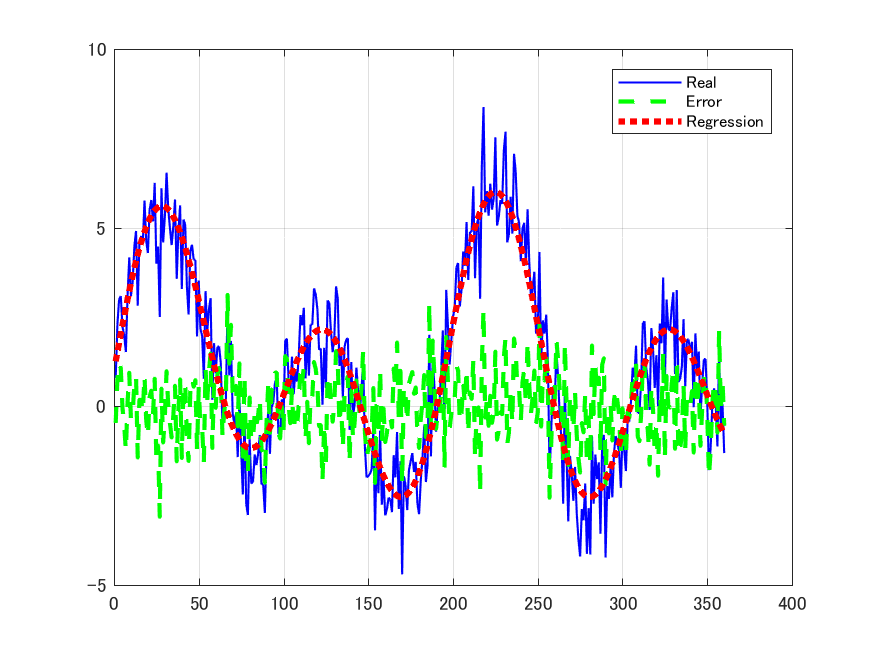
実際の問題は殆どが重回帰分析であるが,重回帰分析は線形代数で表現しないと複雑になる. 線形代数を知らないからと言って,無理に回帰分析を使うと間違いを冒すので,注意が必要である. 以下のプログラム Prog_Rgrs_1.m は,2種類の正弦波とノイズが混じった信号を 回帰分析した例である.
<回帰分析の例>
% Prog_Rgrs_1.mclear;
close;
t = (1:360)'; % 360個のデータを作ります
[m,n] = size(t);
x0 = ones(m,n); % 定数項を分析する説明変数ベクトルです
x1 = sin((pi*t)/90); % 適当な説明変数ベクトルを作ります
x2 = sin((pi*t)/50); % 適当な説明変数ベクトルを作ります
e0 = randn(m,n); % 誤差ベクトル(ノイズ)を作ります
e0 = detrend(e0); % 誤差ベクトル(ノイズ)を作ります
X = [x0,x1,x2]; % 説明変数の列ベクトルを集めて,説明変数行列を作ります
a0 = [1;2;3]; % 未知な係数ベクトルを適当に定めます
y0 = X*a0+e0; % 分析対象となるデータを作ります
H=plot(y0,'b');set(H,'LineWidth',1); % 図を描きます
hold on
H=plot(e0,'g--');set(H,'LineWidth',2); % 図を描きます
H=plot(X*a0,'r:');set(H,'LineWidth',3); % 図を描きます
grid;
H = inv(X'*X)*X'; % 一般化逆行列
ae = H*y0; % 一般化逆行列で求めた解ベクトルを算出します
[a0,ae]
真の解 $\texttt{a0}$ を示す.
a0 =
1.00
2.00
3.00
一般化逆行列で求めた最小2乗解 $\texttt{ae}$ を示す.
真の解 $\texttt{a0}$ と,推定した解 $\texttt{ae}$ が近いことがわかる.
ae =
1.00
2.06
3.06
3.3 データの2乗和を分析する
データ $\bf{y}$ は,式(\ref{Rgrs_eq2})の回帰式に分析できた. ここでは,式(\ref{Rgrs_eq2})で示したデータ ${\bf y}$ の2乗和 ${\bf y^{\rm{T}}} {\bf y}$ を 式(\ref{Rgrs_eq3})のように分析したい. このとき,式(\ref{Rgrs_eq2})の行列 $\bf{X}$ に必要な条件を明らかにする. \begin{equation} \bf{y}^{\rm{T}}\bf{y}=\bf{a}^{\rm{T}}\bf{a}+\bf{e}^{\rm{T}}\bf{e} \label{Rgrs_eq3} \end{equation} 式(\ref{Rgrs_eq2})から,2乗和 ${\bf y^{\rm{T}}} {\bf y}$ は式(\ref{Rgrs_eq3_a})で表すことができる. \begin{eqnarray} {\bf y^{\rm{T}}} {\bf y}&=&({\bf X} {\bf a}+{\bf e})^{\rm{T}} ({\bf X} {\bf a}+{\bf e}) \notag \\ &=&{\bf a^{\rm{T}}} {\bf X^{\rm{T}}} {\bf X} {\bf a}+2{\bf e^t} {\bf X} {\bf a}+{\bf e^{\rm{T}}} {\bf e} \label{Rgrs_eq3_a} \end{eqnarray} 式(\ref{Rgrs_eq2})は回帰式であるから,$\bf{e^{\rm{T}}X}=(0,0,...,0)$ となるので,式(\ref{Rgrs_eq3_a})は式(\ref{Rgrs_eq3_b})に 書き換えられる. \begin{eqnarray} \bf{y}^{\rm{T}} \bf{y}&=& \bf{a}^{\rm{T}} \bf{X}^{\rm{T}} \bf{X} \bf{a}+\bf{e}^{\rm{T}} \bf{e} \label{Rgrs_eq3_b} \end{eqnarray} 式(\ref{Rgrs_eq3})と式(\ref{Rgrs_eq3_b})を比べると式(\ref{Rgrs_eq3_c})が得られる. \begin{eqnarray} \bf{a}^{\rm{T}} \bf{a}&=& \bf{a}^{\rm{T}} \bf{X}^{\rm{T}} \bf{X} \bf{a} \label{Rgrs_eq3_c} \end{eqnarray} よって,$\bf{X}$ は,式(\ref{Rgrs_eq3_d})の条件を満たす直交行列でなくてはならない.なお $\bf{I}$ は単位行列である. \begin{eqnarray} \bf{X}^{\rm{T}} \bf{X}&=& \bf{I} \label{Rgrs_eq3_d} \end{eqnarray}$\textbf{追記3:標準偏差では分析できないことの説明}$
世の中に分散分析という言葉はあっても,標準偏差分析というのは聞いたことが無いように, 標準偏差では分析できない. つまり,RAStoolやTakebarでは,分散を分析した棒グラフを表示している. 一方,よく見かける $3\sigma$ のグラフは,分析ではなく, 全点参照とか,ショット内センター1点参照とか,毎ウエハオフセット除去の全点参照とか, 要するにケーススタディを同じ図に重ねて表示したものと解釈すべきである. 決して,\textbf{分析してはいない}ことに注意すべきである.
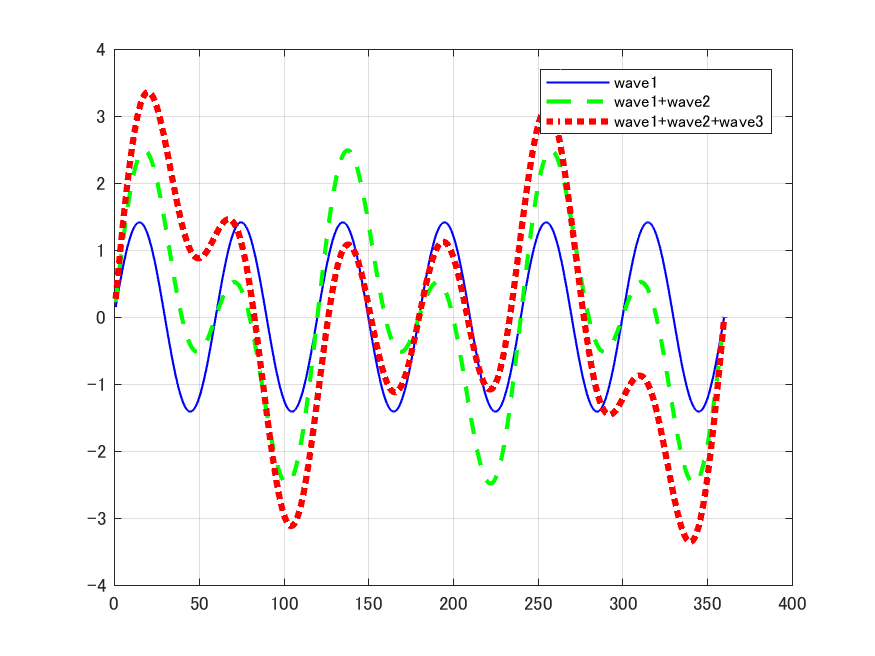
少し,話が横に逸れたが, $\sigma$ の等しい3本の波形を1つずつ合成したとする. 分散だと,2本で2倍,3本で3倍と増加するが,標準偏差 $\sigma$ だとそうはならない. 後から追加したものは小さく見えてしまう. つまり,正しく分析できないのである.
以下のプログラム Prog_Rgrs_2.m は,3種類の正弦波が混じった信号を回帰分析した例である.
% Prog_Rgrs_2.m
clear;
close;
t = (1:360)'; % 360個のデータを作ります
x0 = sqrt(2)*sin((pi*t)/90); % 標準偏差が1のベクトルを作ります
x1 = sqrt(2)*sin((pi*t)/60); % 標準偏差が1のベクトルを作ります
x2 = sqrt(2)*sin((pi*t)/30); % 標準偏差が1のベクトルを作ります
X = [x0,x1,x2]; % 説明変数の列ベクトルを集めて,説明変数行列を作ります
a0 = [0,0,1;0,1,1;1,1,1]; % 各成分を1つ1つ加算して行きます
y0 = X*a0; % 分析対象となるデータを作ります
H=plot(y0(:,1),'b');set(H,'LineWidth',1); % 図を描きます
hold on;
H=plot(y0(:,2),'g--');set(H,'LineWidth',2); % 図を描きます
H=plot(y0(:,3),'r:');;set(H,'LineWidth',3); % 図を描きます
legend('wave1','wave1+wave2','wave1+wave2+wave3');
grid;
print('Rgrs_2','-dpng');
disp(['std(y0)=',num2str(std(y0))]) % 標準偏差は等差級数になりません
disp(['var(y0)=',num2str(var(y0))]) % 分散は等差級数になります
var(y0)=1.0028 2.0056 3.0084
3.4 Shmidtの直交化法
分散を分析するのに直交化が必要なことは,前節で理解されたと思う. ここでは,説明変数行列を直交行列に変換する方法(シュミットの直交化法)を紹介する. この方法を用いると,説明変数行列 $\bf{Z}_{n}$ を構成する列ベクトル $\bf{z}_{j},\ \ j=1,2,\ldots,n$ が互いに独立であれば,必ず直交化できる. 直交行列の第1列 $\bf{x}_{1}$ は式(\ref{Rgrs_eq2_2})で得られる. \begin{equation} \bf{x}_{1}=\frac{\bf{z}_{1}}{\sqrt[]{\mathstrut \bf{z}_{1}^{\rm{T}}\ \bf{z}_{1}}} \label{Rgrs_eq2_2} \end{equation} 第2列目以降は,次の手順で行う.\\ まず,式(\ref{Rgrs_eq2_3})で第j列目の説明変数ベクトル $\bf{z}_{j}$ を重回帰分析して, 残差ベクトル $\bf{e}_{j}$ を求める. \begin{equation} \bf{e}_{j} = \bf{z}_{j} - \bf{Z}_{j-1}[\bf{Z}_{j-1}^{\rm{T}}\ \bf{Z}_{j-1}]^{-1}\bf{Z}_{j-1}^{\rm{T}}\bf{z}_{j} \label{Rgrs_eq2_3} \end{equation} そして,式(\ref{Rgrs_eq2_4})で $\bf{e}_{j}$ を正規化して $\bf{x}_{j}$ を作る. \begin{equation} \bf{x}_{j}=\frac{\bf{e}_{j}}{\sqrt[]{\mathstrut \bf{e}_{j}^{\rm{T}}\ \bf{e}_{j}}} \label{Rgrs_eq2_4} \end{equation} $\bf{x}_{j}$ を直交行列 $\bf{X}_{j}$ の第j列として,$j=n$ となるまで同じ操作を続ければ,直交行列 $\bf{X}_{n}$ ができる. \begin{equation} \bf{X}_{n}=(\bf{x}_{1},\bf{x}_{2},...,\bf{x}_{n}) \label{Rgrs_eq2_5} \end{equation} 例題として,式(\ref{Rgrs_eq2_6})の説明変数行列 $Z$ を直交行列 $X$ にしてみる. \begin{equation} \bf{Z}= \begin{pmatrix} 0 & 1 & 1\\ 1 & 0 & 1\\ 1 & 1 & 0 \label{Rgrs_eq2_6} \end{pmatrix} \end{equation} まず,式(\ref{Rgrs_eq2_2})を用いて第1列 $\bf{x}_{1}$ を求める. \begin{equation} \bf{x}_{1}=\frac{(0\ 1\ 1)^{\rm{T}}} {\sqrt[]{\mathstrut (0\ 1\ 1)\ (0\ 1\ 1)^{\rm{T}} }} = \frac{(0\ 1\ 1)^{\rm{T}}}{\sqrt[]{\mathstrut 2 }}\notag \end{equation} 次に,式(\ref{Rgrs_eq2_3})と式(\ref{Rgrs_eq2_4})を用いて第2列 $\bf{x}_{2}$ を求める. \begin{eqnarray} \bf{e}_{2} &=& \bf{z}_{2} - \bf{Z}_{1}[\bf{Z}_{1}^{\rm{T}}\ \bf{Z}_{1}]^{-1}\bf{Z}_{1}^{\rm{T}}\bf{z}_{2}\notag \\ &=&(1\ 0\ 1)^{\rm{T}}-(0\ 1\ 1)^{\rm{T}} [(0\ 1\ 1) (0\ 1\ 1)^{\rm{T}}]^{-1} (0\ 1\ 1) (1\ 0\ 1)^{\rm{T}}\notag \\ &=&(1\ 0\ 1)^{\rm{T}}-(0\ \ 1/2\ \ 1/2)^{\rm{T}}\notag \\ &=&(1\ \ -1/2\ \ 1/2)^{\rm{T}}\notag \\ \bf{x}_{2}&=&\frac{\bf{e}_{2}}{\sqrt[]{\mathstrut \bf{e}_{2}^{\rm{T}}\ \bf{e}_{2}}} \notag \\ &=&\frac{(1\ \ -1/2\ \ 1/2)^{\rm{T}}}{\sqrt[]{\mathstrut 3/2}}\notag \\ &=&(\sqrt{2/3}\ \ -\sqrt{1/6}\ \ \sqrt{1/6})^{\rm{T}}\notag \end{eqnarray} 同様に,式(\ref{Rgrs_eq2_3})と式(\ref{Rgrs_eq2_4})を用いて第3列 $\bf{x}_{3}$ を求める. \begin{eqnarray} \bf{e}_{3} &=& \bf{z}_{3} - \bf{Z}_{2}[\bf{Z}_{2}^{\rm{T}}\ \bf{Z}_{2}]^{-1}\bf{Z}_{2}^{\rm{T}}\bf{z}_{3}\notag \\ &=&(1\ 1\ 0)^{\rm{T}}- (0\ 1\ 1;\ 1\ 0\ 1) ^{\rm{T}} [(0\ 1\ 1;\ 1\ 0\ 1) (0\ 1\ 1;\ 1\ 0\ 1)^{\rm{T}}]^{-1} (0\ 1\ 1;\ 1\ 0\ 1) (1\ 1\ 0)^{\rm{T}}\notag \\ &=&(1\ 1\ 0)^{\rm{T}}- (0\ 1\ 1;\ 1\ 0\ 1) ^{\rm{T}} (2/3\ \ -1/3;\ -1/3\ \ 2/3) (0\ 1\ 1;\ 1\ 0\ 1) (1\ 1\ 0)^{\rm{T}}\notag \\ &=&(1\ 1\ 0)^{\rm{T}}- (0\ 1\ 1;\ 1\ 0\ 1) ^{\rm{T}} (-1/3\ \ 2/3\ \ 1/3;\ 2/3\ \ -1/3\ \ 1/3) (1\ 1\ 0)^{\rm{T}}\notag \\ &=&(1\ 1\ 0)^{\rm{T}}- (0\ 1\ 1;\ 1\ 0\ 1) ^{\rm{T}} (1/3\ \ 1/3)^{\rm{T}}\notag \\ &=&(1\ 1\ 0)^{\rm{T}}- (1/3\ \ 1/3\ \ 2/3)^{\rm{T}}\notag \\ &=& (2/3\ \ 2/3\ \ -2/3)^{\rm{T}} \notag \\ \bf{x}_{3}&=&\frac{\bf{e}_{3}}{\sqrt[]{\mathstrut \bf{e}_{3}^{\rm{T}}\ \bf{e}_{3}}} \notag \\ &=&\frac{(2/3\ \ 2/3\ \ -2/3)^{\rm{T}}}{\sqrt{4/3}}\notag \\ &=&(\sqrt{1/3}\ \sqrt{1/3}\ -\sqrt{1/3})^{\rm{T}}\notag \end{eqnarray} 以上から \begin{equation} \bf{X}= \begin{pmatrix} 0 & \sqrt{2/3} & \sqrt{1/3}\\ \sqrt{1/2} & -\sqrt{1/6} & \sqrt{1/3}\\ \sqrt{1/2} & \sqrt{1/6} & -\sqrt{1/3} \notag \end{pmatrix} \end{equation}参考に,matlabで書いたShmidtの直交化プログラムを紹介する.
function[Z,TT]=ortho1(N,Zo)
%[Z,TT]=ortho1(N,Zo)
%<機能>
%複数のモード列ベクトルから成る行列に対して、第1列から優先的に順次直交化する。
%<注意>
%列ベクトルの順序を入れ替えると、結果の直交行列は異なる場合がある
%<変数>
% Z:直交化された行列(複数の列ベクトル)
% TT:変換行列(Z=Zo*TT)
% N: 対象となるモードベクトルの範囲
% Zo:元のモード列ベクトルから成る行列
Z=Zo;
TT=eye(N);
for iy=2:N
for ix=1:iy-1
A=Z'*Z;
T=eye(N);
if A(ix,iy)~=0
T(ix,iy)=-sum(Z(:,ix).*Z(:,iy))/sum(Z(:,ix).^2);
Z=Z*T;
TT=TT*T;
end
end
end
問題3.1
次のコマンドを入力して21行4列の説明変数行列 $\texttt{X2}$ と 21行1列の分析対象ベクトル $\texttt{y}$ を作成する.>> x=[-10:10].'; % -10から10までの整数列ベクトル
>> n=length(x); % xの長さ
>> X2=[ones(n,1),x,x.\^2,x.\^3]; % 説明変数行列X2の設定
>> a0=[1;2;3;4]; % 係数ベクトルの設定
>> e=rand(n,1,'normal')*0; % ノイズ生成
>> y=X2*a0+e; % 分析対象ベクトルの作成
また,説明変数行列 $\texttt{X2}$ の1~2列を説明変数行列 $\texttt{X1}$ とする.
>> X1=X2(:,[1,2]); % X1の設定}
このとき,分析対象ベクトル $\texttt{y}$ を説明変数行列 $\texttt{X1}$ と $\texttt{X2}$ の 各々で回帰分析したときの,回帰係数を示せ.
