第11章 機構系モデル
機構解析には,大きく分けて理論解析と実験解析がある. 本章は,図式化した機構系モデルから運動方程式を立てる理論解析の一部分を解説する.機構系に関する多くの教科書は,運動方程式を固有値解析で解き,固有振動数と固有振動モードを求め, 周波数特性を示すまでを説明している. しかし,質点系の機構系モデル(質点とばね,または振り子が連なったもの)から運動方程式を立てる過程は 示されていない.まるで自明のように扱われている.しかし,実はここが難しい. 特に運動方程式における各項の符号(正か負)の付け方が分かりにくい. 質量や慣性モーメントを持ったブロックをばね要素で結合したモデル図は描けても 運動方程式にできなければ,それ以上どうしようもない.
ところが,運動方程式にできれば,後はとても簡単である. ラプラス変換すれば,固有振動数なら中学生の数学力で算出できる.(ラプラス変換自体は少し難しい) 振動モードだって,主成分分析で用いた固有値解析で導くことができる. つまり,教科書で書かれている部分は,完全に理解していなくても余り問題にならない. MATLABやscilabを使えば,僅かな手順でシミュレーションも可能である.
10.1 質点系運動方程式の作り方
質点とばね,ダンパ(速度に比例した力を戻す減速方向に発生させる機構)で 構成されたモデルから運動方程式を作るときは,以下の規則に従えばよい.- (1) 振動が発生する部分に,ばね(及びダンパ)を配置する
- (2) ばねは,質点あるいは固定点に結合する
- (3) 力の運動方程式は,質量×加速度,粘性×速度,剛性×変位,力のいずれかである
- (4) 全質点において変位の方向は等しく定義してある
- (5) 質点の変位を示す変数は,慣性項,粘性項,剛性項において同符号である
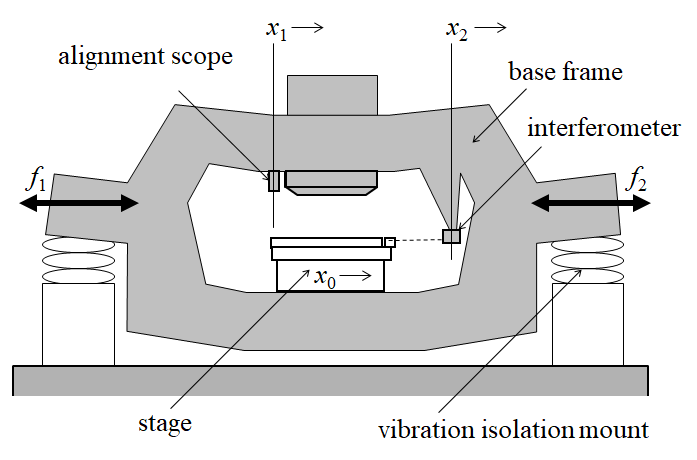
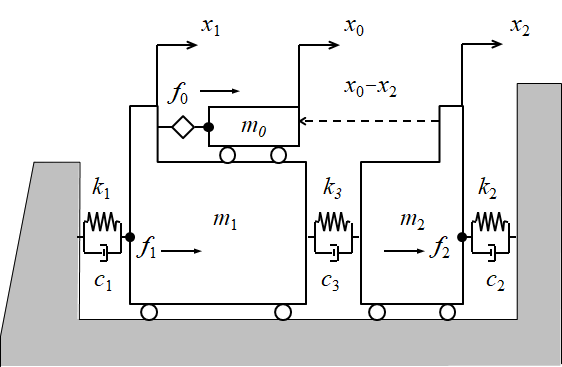
図11.2は,本体変形による干渉計の計測騙されを示す質点系モデルである. この場合,アライメントスコープや投影レンズと干渉計との変位があるので,本体構造を 2つの質点 $m_{1}$ と $m_{2}$ に分割し,その間にばね $k_{3}$ を配置した. ステージを示す質点 $m_{0}$ はリニアモータからの駆動力 $f_{0}$ を受けるだけなので,ばねを持たない. なお,除振系は $k_{1}$ と $k_{2}$ の2つのばねで表した. また,ころのイメージは摩擦の無いガイドを意味する.
さて,各質点について運動方程式を作る. $m_{0}$ の運動方程式は簡単である.質点と加速度 $\ddot{x_{0}}$ との積が慣性力となる. そして,慣性力は与えられた駆動力 $f_{0}$ と釣り合うので式(\ref{eq1107_1})となる. \begin{equation} m_{0}\ddot{x_{0}}=f_{0} \label{eq1107_1} \end{equation} 質点 $m_{1}$ には,2つのばねが結合しているから,これらのばねの伸縮力が $m_{1}$ に作用する. 外力としてはステージ駆動反力 $-f_{0}$ が作用する. よって,式(\ref{eq1107_2})のように表される.ただし,$\pm$ は正負の符号が不明であることを意味する. \begin{equation} m_{1}\ddot{x_{1}} \pm c_{1}\dot{x}_{1} \pm c_{3}(\dot{x}_{1}-\dot{x}_{2}) \pm k_{1}x_{1} \pm k_{3}(x_{1}-x_{2}) =-f_{0} \label{eq1107_2} \end{equation} 規則(5)によれば,$\ddot{x}_{1}$,$\dot{x}_{1}$,$x_{1}$ は同符号で作用するから, 式(\ref{eq1107_2})は式(\ref{eq1107_3})になる. \begin{equation} m_{1}\ddot{x_{1}} + c_{1}\dot{x}_{1} + c_{3}(\dot{x}_{1}-\dot{x}_{2}) + k_{1}x_{1} + k_{3}(x_{1}-x_{2}) =-f_{0} \label{eq1107_3} \end{equation} 質点 $m_{2}$ にも,2つのばねが結合しているが外力は作用しない. よって,式(\ref{eq1107_4})のように表される. \begin{equation} m_{2}\ddot{x_{2}} \pm c_{2}\dot{x}_{2} \pm c_{3}(\dot{x}_{1}-\dot{x}_{2}) \pm k_{2}x_{2} \pm k_{3}(x_{1}-x_{2}) =0 \label{eq1107_4} \end{equation} 同様に規則(5)によれば,$\ddot{x}_{2}$,$\dot{x}_{2}$,$x_{2}$ は同符号で作用するから, 式(\ref{eq1107_4})は式(\ref{eq1107_5})になる. \begin{equation} m_{2}\ddot{x_{2}} + c_{2}\dot{x}_{2} - c_{3}(\dot{x}_{1}-\dot{x}_{2}) + k_{2}x_{2} - k_{3}(x_{1}-x_{2}) =0 \label{eq1107_5} \end{equation} 大切なのは"規則(5)"である.これさえ知っていれば,正しい運動方程式を作ることができる.
10.2 回転と並進の運動方程式
現実の振動は並進だけでなく回転を伴うことが多い. ここでは,回転と並進の両方を持った機構系モデルの運動方程式を作る. まず,図11.3に示すような,ダンパを省略した単純な例を考える.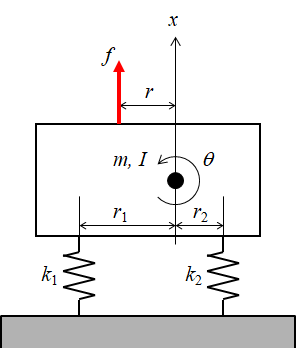
質点系モデルは,回転運動も並進運動も重心について定義する. つまり,重心における並進と回転だけを考えるから,重心に質量 $m$ と慣性モーメント $I$ が 集中しているモデルになる. 図11.3の場合,ばねの作用力線と重心との距離は各々 $r_{1}$ と $r_{2}$ である.
さて,重心における並進の運動方程式は,力の釣り合いを示すので式(\ref{eq1107_6})になる. \begin{equation} m\ddot{x}+k_{1}(x-r_{1}\theta)+k_{2}(x+r_{2}\theta)=f \label{eq1107_6} \end{equation} 一方,重心における回転の運動方程式は,モーメントの釣り合いを示す必要がある. つまり,運動方程式を構成する要素は,慣性モーメント×角加速度,粘性×速度×距離,剛性×変位×距離に なるので,その運動方程式は(\ref{eq1107_7})になる. なお,回転方向は反時計回り方向を正とするのが一般的である. \begin{equation} I\ddot{\theta} \pm k_{1}\ (x-r_{1}\theta)\ r_{1} \pm k_{2}(x+r_{2}\theta)\ r_{2}= -fr \label{eq1107_7} \end{equation} 式(\ref{eq1107_7})でも,各項の符号決定には規則(5)を用いる. この場合,$\ddot{\theta}$ と $\theta$ の項が同符号になるので,回転の運動方程式は式(\ref{eq1107_8})になる. \begin{equation} I\ddot{\theta} - k_{1}\ (x-r_{1}\theta)r_{1} + k_{2}(x+r_{2}\theta)\ r_{2}= -fr \label{eq1107_8} \end{equation}
問題11.1
図11.4の機構系モデル図から,各質点の運動方程式を立てる.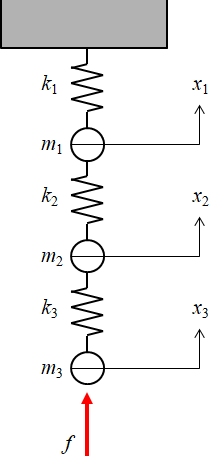
問題11.2
図11.5の機構系モデル図から,各質点の運動方程式を立てる.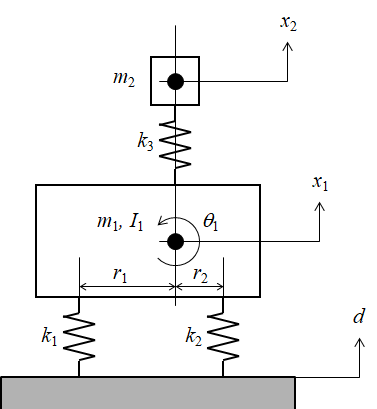
問題11.3
図11.6の機構系モデル図から,各質点の運動方程式を立てる.