第13章　最適化手法

　バランスの良い設計や適切な改善策の提案を行うには，システムの特徴を捉えた数学モデルが役立つ． しかし，構成要素を変えずにシステムの改良を考えるなら，最適化手法の知識が必要になる． 特に，露光装置の調整では必ず最適化が行われるから，これに関わる者には重要なテーマである．
　本章は，使用頻度が高くて，簡単に使える最適化手法を紹介する．
　第一は重み付き最小2乗法である．単純で使いやすいため，広く用いられている． 第二は線形計画法による最大絶対値最小化である． ディストーションの最適調整に用いてから，光学系の調整に多用されている． これは，全ての規格を満足させるような調整問題に適しており，汎用性が高い． 第三は非線形計画問題である．多変数の場合は専用のソルバーを用いて計算するが， 演算時間も長く満足できる解も得られないことが多い．しかし，工夫して線形問題や 1変数問題に置き換えれば，割と簡単に良い解が得られる． ここでは，そうした事例を紹介する．

13.1　重み付き最小2乗法

　重み付き最小2乗法で扱うのは，式(\ref{Optm_eq1})のような線形モデルである． \begin{equation} \bf{W\ e}=\bf{W\ y}-\bf{W\ A\ x} \label{Optm_eq1} \end{equation} 　$\bf{e}$ は残差列ベクトル，$\bf{W}$ は重みを与える対角行列で，対角要素は全て非負である． $\bf{y}$ は補正対象列ベクトル，$\bf{A}$ は補正行列で $\bf{x}$ は未知の制御ベクトルである． 最小2乗法は，重み付き残差ベクトルの内積 $\bf{e^{\rm{T}}\ W^{\rm{T}}\ W\ e}$ を最小とするように $\bf{x}$ を定める． $\bf{e^{\rm{T}}\ W^{\rm{T}}\ W\ e}$ は正値で，下に凸であることが保証されるので， $\bf{e^{\rm{T}}\ W^{\rm{T}}\ W\ e}$ の極値を探す． つまり，式(\ref{Optm_eq2})に示すように，制御ベクトル $\bf{x}$ の要素である $x_{i}$ で $\bf{e^{\rm{T}}\ W^{\rm{T}}\ W\ e}$ を偏微分した値が 全て0になる制御ベクトル $\bf{x}$ を求めればよい．
\begin{eqnarray} \frac{\partial}{\partial\bf{x}}\bf{e^{\rm{T}}\ W^{\rm{T}}\ W\ e}&=&\frac{\partial}{\partial\bf{x}}\bf{y^{\rm{T}}\ W^{\rm{T}}\ W\ y} -2\frac{\partial}{\partial\bf{x}}\bf{x^{\rm{T}}\ A^{\rm{T}}\ W^{\rm{T}}\ W\ y} +\frac{\partial}{\partial\bf{x}}\bf{x^{\rm{T}}\ A^{\rm{T}}\ W^{\rm{T}}\ W\ A\ x}\notag \\ \notag \\ &=&-2\bf{\ A^{\rm{T}}\ W^{\rm{T}}\ W\ y}+2\bf{\ A^{\rm{T}}\ W^{\rm{T}}\ W\ A\ x}=\bf{0} \label{Optm_eq2} \end{eqnarray} 　式(\ref{Optm_eq3})を解けば，未知の制御ベクトル $\bf{x}$ が求められる． \begin{equation} \bf{x}=(\bf{A^{\rm{T}}\ W^{\rm{T}}\ W\ A})^{-1}\bf{A^{\rm{T}}\ W^{\rm{T}}\ W\ y} \label{Optm_eq3} \end{equation} 　matlabなら，以下のコマンドで最小2乗解が得られる．

>> x=inv(A'*W'*W*A)*A'*W*y};

　あるいは，以下のようにムーアペンローズの擬似逆行列を用いてもよい．

>> x=pinv(W*A)*W*y};

　最小2乗法は，ガウスが考案した方法だけあって，色々な面でよく出来ている． 第一に最適化の対象が連立1次方程式で表現され単純である． 第二に極値（微分値が0である点）を探すというのは理解しやすい． 第三に計算が簡単で使いやすい． だから，最小2乗法は最適化手法の王様だと思う．
　他にも，「もし，最適解であればどうなるか？」という考え方を導入した点が素晴らしい． 探索法を避けた最小2乗法の考え方は，最適解法を考える上で大変参考になる．

13.2　線形計画法

　最小2乗法に比べると線形計画法は使いにくい． それは，線形計画法の標準形をそのまま使える問題が少ないからである． ところが，線形計画法を応用した最大絶対値最小化の表現は，最小2乗法と目的が似ており使いやすく感じる．
　先ず，最大絶対値最小化を実現する表現を式(\ref{Optm_eq4})と(\ref{Optm_eq5})に示す． \begin{equation} \rm{minimize\ :}\ \ \ t \label{Optm_eq4} \end{equation} \begin{equation} \rm{subject\ to\ :}\ \ \ \ |\bf{b}-\bf{A\ x}|\leq t \label{Optm_eq5} \end{equation} 　式(\ref{Optm_eq4})で最小化する $t$ は，実体のないダミー変数である． そして，このダミー変数より小さいか等しいという制約条件によって， 式(\ref{Optm_eq5})の絶対値 $|\bf{b}-\bf{A\ x}|$ を最小化するのである．
　一方，線形計画法の標準形は式(\ref{Optm_eq6})～(\ref{Optm_eq8})で表される． \begin{equation} \rm{minimize\ :}\ \ \ \bf{f^{\rm{T}}} x \label{Optm_eq6} \end{equation} \begin{equation} \rm{subject\ to\ :}\ \ \ \ \bf{A\ x}\leq \bf{b} \label{Optm_eq7} \end{equation} \begin{equation} \ \ \bf{x}\geq \bf{0} \label{Optm_eq8} \end{equation} 　式(\ref{Optm_eq8})に「変数 $x$ は非負である」という条件がある． 式(\ref{Optm_eq7})の $\bf{A\ x}\leq \bf{b}$ という制約条件も余りピンと来ない． 式(\ref{Optm_eq6})の目的関数が制御変数の線形和 $\bf{f^{\rm{T}}\ x}$ というのも考えにくい．
　しかし，多くの計算ソフトでは標準形で表現することが求められる． そのため，標準形から式(\ref{Optm_eq4})と(\ref{Optm_eq5})の最大絶対値最小化の表現に変更するには， ちょっとした技法が必要となる． まず，非負でない変数ベクトル $\bf{x}$ を表すには，同じ大きさの非負ベクトル $\bf{x}_{1}$ と $\bf{x}_{2}$ を用意して，$\bf{x}=\bf{x}_{1}-\bf{x}_{2}$ と定義する． 次に，制約条件に含まれる絶対値表現 $|\bf{b}-\bf{A\ x}|\leq t$ は， $\bf{b}-\bf{A\ x}\leq t$ と $-\bf{b}+\bf{A\ x}\leq t$ という表現をする．
　matlabを使えば，列ベクトル $|\bf{y}-\bf{Ax}|$ の最大絶対値を最小化する解 $\bf{x}$ は， 次のようにして得られる．

>> f = [zeros(size(x));1];
>> AA = [A,-ones(size(y,1),size(y,2));-A,-ones(size(y,1),size(y,2))];
>> b = [y;-y];
>> xx = linpro(f,AA,b);
>> x = xx(1:length(xx)-1);

　さて，上のプログラムを説明する． 1行目は目的関数をダミー変数だけにしている． 2,3行目は，絶対値の最小化を表すように制約条件を設定し，4行目で線形計画法を解いている． なお，matlabでは，x の非負条件を無視して構わないので，プログラムに書く必要はない． そして，5行目で変数 $x$ を $xx$ から取り出している． ここで取り除かれた $xx(length(xx))$ はダミー変数である．
　これも個人的な意見であるが，「線形計画法による最大絶対値最小化」は最小2乗法に次いで有用である． それは，最大絶対値最小化の解法が，全ての評価項目を許容範囲に設定する設計や調整の問題に適用できるからである．

13.3　非線形問題

　最小2乗法や線形計画法を用いる場合は，変数の変動範囲を限定して， 非線形問題を線形モデルに近似していることが多い． 対象を線形モデルで近似したり単純化することは，技術に工学を応用する導入部である． 従って，何も考えずに多変量の非線形計画問題をそのまま非線形計画法で解くのはよろしくない． ちょっとした工夫で線形計画問題に置き換えられる場合も多い． たとえ，線形計画問題にできなくても，多変数問題を1変数問題に置き換えれるかも知れない． こうした工夫が行うと，短い演算時間で良い解が得られる． いきなりEXCELのソルバーに頼るようなことは避けるべきである． 私達工学技術者は，そうした努力が必要なのである． ここでは，多変数の非線形問題を線形問題および1変数の非線形問題に置き換えた事例を 紹介する．

線形問題に置き換えた事例

　これは，離散的に計測した $n$ 箇所の外周位置データ $(x_{i},y_{i}),\ \ i=1,...,n$ から， 円の中心 $(x_{0},y_{0})$ と半径 $r$ を求める問題である． 図13.1に具体例を示す．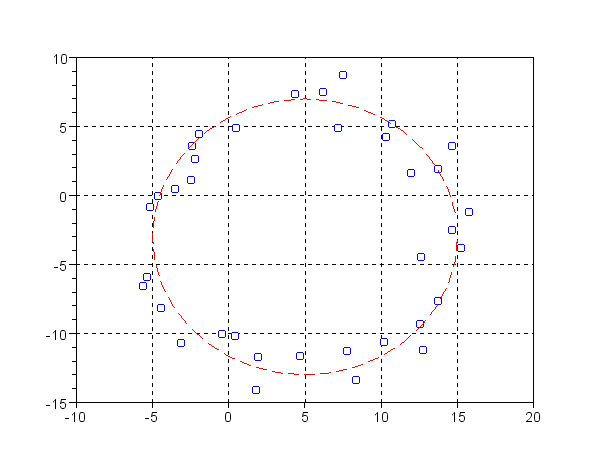

　これを数学的に表せば，式(\ref{Optm_eq9})のようになる． なお，$e_{i}$ は残差である．
\begin{equation} (x_{i}-x_{0})^{2}+(y_{i}-y_{0})^{2}=r^{2}+e_{i} , \hspace{20mm}i=1,...,n \label{Optm_eq9} \end{equation} 　これは，式(\ref{Optm_eq10})のように表される． \begin{equation} (x_{i}^{2}+y_{i}^{2})-e_{i} = 2x_{i}x_{0} +2y_{i}y_{0} -x_{0}^{2}-y_{0}^{2}+r^{2}, \hspace{20mm}i=1,...,n \label{Optm_eq10} \end{equation} 　$z_{0}=r^{2}-x_{0}^{2}-y_{0}^{2}$ とすれば，これは $x_{0}$，$y_{0}$，$z_{0}$ を未知数とする 連立１次方程式になる．$\sum_{i=1}^{n}e_{i}^{2}$ を最小にする解を求めるなら，最小2乗法で解けばよい． また，max($e_{i}$)を最小にする解を求めるなら，「線形計画法による最大絶対値最小化」で解けばよい．
　参考に，最小2乗法と線形計画法の2つの解を求め，図13.1を描くmatlabのプログラムを示す．

***************************************************************
>> % 円重心と真円度中心を求める
>> clear;% メモリ消去
>> xdel(winsid());% 図の消去
>> s = (\%pi*(10:10:360)')/180;% 角度ベクトルの定義
>> [m,n]=size(s);
>> r = 10;% 半径
>> x0 = 5;% 円中心ｘ座標
>> y0 = -3;% 円中心ｙ座標
>> dx = rand(m,n,"normal");% 誤差ベクトル
>> dy = rand(m,n,"normal");% 誤差ベクトル
>> x = r*cos(s)+x0*ones(m,n);% 円周点の真値
>> y = r*sin(s)+y0*ones(m,n);% 円周点の真値
>> x1 = x+dx;% 円周点の計測値
>> y1 = y+dy;% 円周点の計測値
>> % 最小2乗法で円重心を求める
>> z = x1 .\^\ 2+y1 .\^\ 2;
>> A = [2*x1,2*y1,ones(m,n)];
>> f0 = inv(A.'*A)*A.'*z;
>> x00 = f0(1);
>> y00 = f0(2);
>> r00 = sqrt(f0(3)+f0(1)\^\ 2+f0(2)\^\ 2);
>> % 線形計画法で真円度を求める
>> f1 = [0;0;0;1];
>> N = max(size(x1));
>> AA = [-A,-ones(N,1);A,-ones(N,1)];
>> b = [-z;z];
>> pp = linpro(f1,AA,b);
>> x10 = pp(1);
>> y10 = pp(2);
>> r10 = sqrt(pp(3)+pp(1)\^\ 2+pp(2)\^\ 2);
>> square(-1,-1,1,1);
>> plot(x1,y1,"o",x,y,"r--")
>> xgrid(2)
***************************************************************

1変数の非線形問題に置き換えた事例

　ここでは，線幅からベストフォーカス位置を探る問題を例に， \textbf{ニュートン法による1変数非線形問題}を説明する． 合焦の状態によって像の線幅は変化し，ベストフォーカス位置で最大となる． そのため，$n$ 箇所のフォーカス位置 $x_{i}$ で計測した線幅 $y_{i}$ は式(\ref{Optm_eq11})で表される． なお，$e_{i}$は残差である．
\begin{equation} y_{i}=a(x_{i}-v)^{4}+b(x_{i}-v)^{2}+c+e_{i} , \hspace{20mm}i=1,...,n \label{Optm_eq11} \end{equation} 　例題では，真のベストフォーカス $v$ は-0.547，各係数 $[a,b,c]$ は $[-1, 1, 1]$ であるとしてシミュレーションを行った. このとき得られた線幅 $y_{i}$ を図13.2に示す．

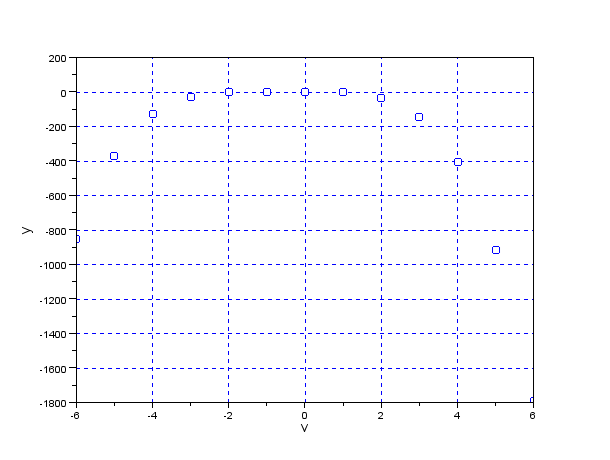
　問題は，残差 $e_{i}$ の2乗和が最小になるよう，未知なベストフォーカス位置 $v$ と， 各係数 $a$，$b$，$c$ を導くことにある． そのまま線形化はできないが，$v$ が与えられれば線形モデルになるから， $a$，$b$，$c$ は最小2乗法で求められる． つまり，$v$ だけを探索する1変数の非線形計画問題として解ける． この場合，目的関数 $f(v)$ は，式(\ref{Optm_eq12})で表せる．
\begin{equation} f(v)=\sum^{n}_{i=1}\{y_{i}-a(x_{i}-v)^{4}-b(x_{i}-v)^{2}-c\}^{2} , \hspace{20mm}i=1,...,n \label{Optm_eq12} \end{equation} 　こういう探索で便利なのがニュートン法である． $f(v)$ が極小にあるなら，その1次導関数 $f'(v)$ が零で，2次導関数 $f''(v)$ は正であるから， そういう条件を満たす $v$ を探索する．
　図13.3に目的関数 $f(v)$ を，図13.4に1次導関数 $f'(v)$ を示す． 4次関数なので極値は3つ存在し，与えたとおりに $v=-0.547$ で最小になっている． なお，丸印が付いている範囲は2次導関数 $f''(v)$ 正の部分である．

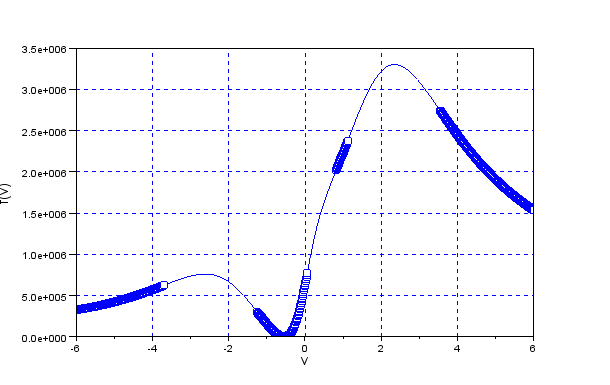
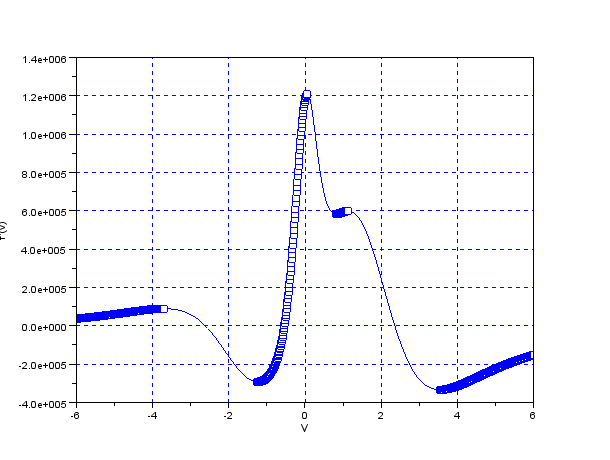
図13.5に2次導関数$f''(v)$を示す．

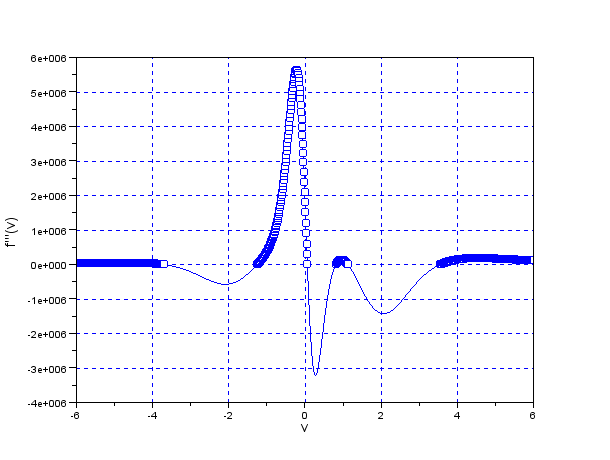
　導関数 $f'(v)$，$f''(v)$ は微小な範囲 $dv$ を用いれば，式(\ref{Optm_eq13})，(\ref{Optm_eq14})で近似できる．
\begin{eqnarray} f'(v)&=&\frac{f(v+dv)-f(v)}{dv} \label{Optm_eq13} \\ f''(v)&=&\frac{f(v+dv)-2f(v)+f(v-dv)}{dv^{2}} \label{Optm_eq14} \end{eqnarray} 　探索する手順は， 最初に大まかな間隔で範囲全体を走査し，2次導関数 $f''(v)$ が正になる 連続した範囲を求めておく．
　次に，求めた範囲で適当な初期値 $v$ を与え，そこから $v+u$ に移動したときの 1次導関数を $f'(v+u)$ を式(\ref{Optm_eq15})で近似する．
\begin{equation} f'(v+u)=f'(v)+f''(v)u \label{Optm_eq15} \end{equation} 　次に探索すべき位置 $v+u$ は，近似した右辺が0となるから，$u$ は式(\ref{Optm_eq16})で表される． \begin{equation} u=-\frac{f'(v)}{f''(v)} \label{Optm_eq16} \end{equation} 　式(\ref{Optm_eq16})で移動量 $u$ を決め，$f'(v+u)$ が0に十分近づくまで繰り返す． こうすれば，多峰性の関数でも最適解の候補が求められるから， 最後に $f(v)$ の最も小さい候補解を選べばよい．

13.4　その他の最適化問題

　恐らく，多くの最適化問題は最小2乗法で済む． 残りは，線形計画法による最大絶対値最小化と非線形計画問題の取り扱いを少し 知っていれば良い．もし満足できないなら，3ヶ月位は調査と試行錯誤で頑張るべきである． それでも満足できないなら一流の専門家に頼るのが良い．
　東京農工大との共同研究は，2000年のディストーション調整から始まって，レンズ群回し調整，非球面レンズの設計， ＭＡＸの最適な制御目標値算出，高次重ね合せ補正やショット順など，露光装置三大性能（解像力，重ね合わせ精度，スループット）の全てに絶大な貢献をした．
　これらのアイデアは私達の知識では思いつかない，とても専門的なものである． こうした方法を学び，自ら取り組む姿勢は大切である． しかし，専門家の力を上手に活用できないと技術競争には勝てない． 依頼すべき専門家を見出し，適切な課題を提示する能力も重要である．